摘要:示数(V)
网址:http://m.1010jiajiao.com/timu_id_587987[举报]
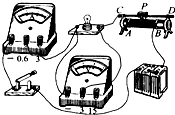 图所示某同学做“测定一个小灯泡的功率”的实验,所用灯泡的额定电压是2.2V.
图所示某同学做“测定一个小灯泡的功率”的实验,所用灯泡的额定电压是2.2V.(1)连接电路时,开关应处于
断开
断开
状态,闭合开关前,变阻器的滑片P应处于C
C
端(选填C或D).(2)实际实验的有关记录与计算如下表:从表中可知,该小灯泡的额定功率是
0.48W
0.48W
.该同学注意到灯的亮度变化是:第二次比第一次暗,第三次比第一次更亮.你认为,根据他观察的现象和实验数据分析,可得出的结论是灯泡亮度由灯泡实际功率决定,实际功率越大,灯泡越亮
灯泡亮度由灯泡实际功率决定,实际功率越大,灯泡越亮
.(3)他还注意到实验记录也可以用来计算灯丝的电阻,完成的有关计算如下表:
这位同学有些纳闷:导体的电阻不是与电压、电流无关吗,怎么三次计算的灯丝电阻却不一样呢?请你对此作一种可能性的
解释:
灯泡电阻受温度影响
灯泡电阻受温度影响
.| 实验次数 | 1 | 2 | 3 |
| 电压(V) | 2.2 | 1.5 | 2.5 |
| 电流(A) | 0.22 | 0.16 | 0.24 |
| 功率(W) | 0.48 | 0.24 | 0.60 |
| 实验次数 | 1 | 2 | 3 |
| 电压(V) | 2.2 | 1.5 | 2.5 |
| 电流(A) | 0.22 | 0.16 | 0.24 |
| 灯丝电阻(Ω) | 10.0 | 9.38 | 10.4 |
图所示的装置很有创意--它将比较耗水的洗衣机和同样耗水但不太讲究水质的马桶连在一起:上部是洗衣机(有关技术参数见铭牌),下部是马桶,中间设有贮水箱.洗衣机还设有加热功能,洗涤前先将水加热到适宜温度,可以提高洗涤效果.
(1)冲一次马桶需要5L水,若一次洗衣服用的总水量是50kg,则可供冲马桶几次?
(2)求脱水时的正常工作电流
(3)某次洗衣时,首次进水量为15kg,正常加热15min水温达到设定要求.求:
①加热过程消耗的电能;
②若加热时电能的80%转化为水的内能,求水升高的温度.[c水=4.2×l03J/(kg?℃),g取10N/kg].
查看习题详情和答案>>

(1)冲一次马桶需要5L水,若一次洗衣服用的总水量是50kg,则可供冲马桶几次?
(2)求脱水时的正常工作电流
| ××滚筒式洗衣机 | |
| 电压/V | 220 |
| 洗衣功率/W | 200 |
| 脱水功率/W | 330 |
| 最大洗涤容量/kg | 5 |
| 水加热功率/W | 2000 |
①加热过程消耗的电能;
②若加热时电能的80%转化为水的内能,求水升高的温度.[c水=4.2×l03J/(kg?℃),g取10N/kg].
 图所示的是测量小灯泡电功率实验电路.所用灯泡额定电压为2.5V,灯丝电阻约10Ω,电源电压4.5V.
图所示的是测量小灯泡电功率实验电路.所用灯泡额定电压为2.5V,灯丝电阻约10Ω,电源电压4.5V.(1)请用笔画线代替导线将图中的电路连接完整.
(2)连接电路过程中,开关应
断开
断开
,接通电路前还应把滑动变阻器滑片调节到B
B
端.(3)下表为某次实验记录的数据及其处理结果.
数据记录及处理表格
| 电压(V) | 灯泡 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | |
| 变阻器 | 4 | 3.5 | 3 | 2.5 | 2 | 1.5 | ||
| 电 流(A) | 0.08 | 0.13 | 0.17 | 0.18 | 0.2 | 0.22 | ||
| 电功率(W) | 灯泡 | 0.04 | 0.13 | 0.26 | 0.36 | 0.5 | 0.66 | |
| 变阻器 | 0.32 | 0.46 | 0.51 | 0.45 | 0.4 | 0.33 | ||
②小灯泡的额定功率为
0.5
0.5
W.②滑动变阻器的电功率随其阻值的变化规律是
电阻从大到小变化时,电功率先变大后变小,中间一定有个最大值
电阻从大到小变化时,电功率先变大后变小,中间一定有个最大值
.电路的总功率随变阻器阻值的变化规律是
变阻器阻值越大,总功率越小
变阻器阻值越大,总功率越小
.③本实验中多次测量电流和电压值是为了
获取多组数据,便于发现规律
获取多组数据,便于发现规律
. 在瓶中装满水后,将它放在水平地面上,如图(a)所示.(g取10N/Kg)求:
在瓶中装满水后,将它放在水平地面上,如图(a)所示.(g取10N/Kg)求: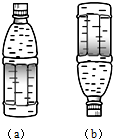 表中数据为一个空瓶的质量、容积等各项参数.在瓶中装满水后,将它放在水平地面上,如图(a)所示.求:
表中数据为一个空瓶的质量、容积等各项参数.在瓶中装满水后,将它放在水平地面上,如图(a)所示.求: