摘要：已知点B1(1.y1).B2(2.y2).-.Bn(n.yn).-(n∈N*)顺次为直线y＝+上的点.点A1(x1.0).A2(x2.0).-An(xn.0).-(n∈N*)顺次为x轴上的点.其中x1＝a.对任意的n∈N*.点An.Bn.An+1构成以Bn为顶点的等腰三角形．(Ⅰ)证明:数列{yn}是等差数列,(Ⅱ)求证:对任意n∈N*.x n+2-x n是常数.并求数列{x n}的通项公式,(Ⅲ)在上述等腰三角形A nB nA n+1中是否存在直角三角形.若存在.求出此时a的值,若不存在.请说明理由．
网址：http://m.1010jiajiao.com/timu_id_572314[举报]
已知点B1（1，y1），B2（2，y2），…，Bn（n，yn）（n∈N*）在直线y=
x+1上，点A1（x1，0），A2（x2，0），A3（x3，0），…，An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶角的等腰三角形，设△AnBnAn+1的面积为Sn，
（1）证明：数列{yn}是等差数列；
（2）求S2n-1（用a和n的代数式表示）；
（3）设数列{
}前n项和为Tn，判断Tn与
（n∈N*）的大小，并证明你的结论．
查看习题详情和答案>>
| 1 |
| 2 |
（1）证明：数列{yn}是等差数列；
（2）求S2n-1（用a和n的代数式表示）；
（3）设数列{
| 1 |
| S2n-1S2n |
| 8n |
| 3n+4 |
已知点B1（1，y1），B2（2，y2），…，Bn（n，yn），…（n∈N*）顺次为直线y=
+
上的点，点A1（x1，0），A2（x2，0），…An（xn，0），…（n∈N*）顺次为x轴上的点，其中x1=a（0＜a＜1），对任意的n∈N*，点An、Bn、An+1构成以Bn为顶点的等腰三角形．
（Ⅰ）证明：数列{yn}是等差数列；
（Ⅱ）求证：对任意的n∈N*，xn+2-xn是常数，并求数列{xn}的通项公式；
（Ⅲ）在上述等腰三角形AnBnAn+1中是否存在直角三角形，若存在，求出此时a的值；若不存在，请说明理由．
查看习题详情和答案>>
| x |
| 4 |
| 1 |
| 12 |
（Ⅰ）证明：数列{yn}是等差数列；
（Ⅱ）求证：对任意的n∈N*，xn+2-xn是常数，并求数列{xn}的通项公式；
（Ⅲ）在上述等腰三角形AnBnAn+1中是否存在直角三角形，若存在，求出此时a的值；若不存在，请说明理由．
已知点B1（1，y1），B2（2，y2），…，Bn（n，yn）（n∈N*）在直线y=
x+1上，点A1（x1，0），A2（x2，0），A3（x3，0）…An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶点的等腰三角形，设△AnBnAn+1的面积为Sn．
（1）证明：数列{yn}是等差数列；
（2）求S2n-1（用n和a的代数式表示）．
查看习题详情和答案>>
| 1 | 2 |
（1）证明：数列{yn}是等差数列；
（2）求S2n-1（用n和a的代数式表示）．
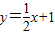上，点A1（x1，0），A2（x2，0），A3（x3，0），…，An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶角的等腰三角形，设△AnBnAn+1的面积为Sn，
前n项和为Tn，判断Tn与
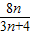（n∈N*）的大小，并证明你的结论．
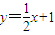上，点A1（x1，0），A2（x2，0），A3（x3，0），…，An（xn，0）顺次为x轴上的点，其中x1=a（0＜a＜1），对于任意n∈N*，点An，Bn，An+1构成以∠Bn为顶角的等腰三角形，设△AnBnAn+1的面积为Sn，
前n项和为Tn，判断Tn与
（n∈N*）的大小，并证明你的结论．