题目内容
已知点B1(1,y1),B2(2,y2),…,Bn(n,yn)(n∈N*)在直线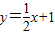 上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn,
上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn,(1)证明:数列{yn}是等差数列;
(2)求S2n-1(用a和n的代数式表示);
(3)设数列
 前n项和为Tn,判断Tn与
前n项和为Tn,判断Tn与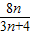 (n∈N*)的大小,并证明你的结论.
(n∈N*)的大小,并证明你的结论.
【答案】分析:(1)由数列的函数特性,要证明数列{yn}是等差数列,我们可以根据已知点B1(1,y1),B2(2,y2),…,Bn(n,yn)(n∈N*)在直线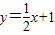 上,进而给出数列{yn}的通项公式,利用通项公式法证明.
上,进而给出数列{yn}的通项公式,利用通项公式法证明.
(2)由已知易得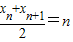 ,进一步可以证明数列{xn}所有的奇数项成等差数列,所有的偶数项也成等差数列,由等差数列的性质易得A2n-1(2n+a-2,0),A2n(2n-a,0),结合(1)的结论和三角形面积公式,即可给出S2n-1的表达式.
,进一步可以证明数列{xn}所有的奇数项成等差数列,所有的偶数项也成等差数列,由等差数列的性质易得A2n-1(2n+a-2,0),A2n(2n-a,0),结合(1)的结论和三角形面积公式,即可给出S2n-1的表达式.
(3)由(2)的结论,易给出数列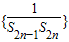 前n项和为Tn的表达式,利用裂项求和法,化简Tn的表达式再与
前n项和为Tn的表达式,利用裂项求和法,化简Tn的表达式再与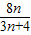 进行比较,即可得到结论.
进行比较,即可得到结论.
解答:解:(1)由于点B1(1,y1),B2(2,y2),,Bn(n,yn)(n∈N*)在直线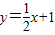 上,
上,
则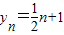 ,
,
因此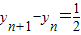 ,所以数列{yn}是等差数列;
,所以数列{yn}是等差数列;
(2)由已知有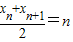 ,那么xn+xn+1=2n,同理xn+1+xn+2=2(n+1),
,那么xn+xn+1=2n,同理xn+1+xn+2=2(n+1),
以上两式相减,得xn+2-xn=2,
∴x1,x3,x5,…,x2n-1,成等差数列;x2,x4,x6,…,x2n,也成等差数列,
∴x2n-1=x1+(n-1)×2=2n+a-2,x2n=x2+(n-1)×2=(2-a)+(n-1)×2=2n-a,
点A2n-1(2n+a-2,0),A2n(2n-a,0),
则|A2n-1A2n|=2(1-a),|A2nA2n+1|=2a,
而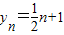 ,
,
∴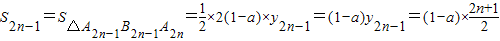 ;
;
(3)由(2)得: ,
,
则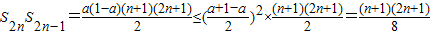
而S2nS2n-1>0,则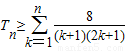 ,
,
即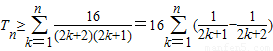
∴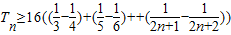
∴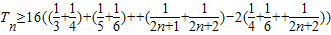
∴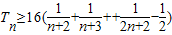
由于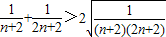 ,
,
而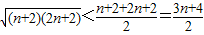 ,
,
则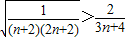 ,从而
,从而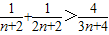 ,
,
同理:
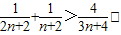
以上n+1个不等式相加得: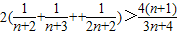
即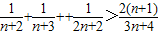 ,
,
从而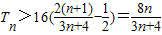 .
.
点评:要判断一个数列是否为等差(比)数列,我们常用如下几种办法:①定义法,判断数列连续两项之间的差(比)是否为定值;②等差(比)中项法,判断是否每一项都是其前一项与后一项的等差(比)中项;③通项公式法,判断其通项公式是否为一次(指数)型函数;④前n项和公式法.
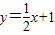 上,进而给出数列{yn}的通项公式,利用通项公式法证明.
上,进而给出数列{yn}的通项公式,利用通项公式法证明.(2)由已知易得
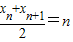 ,进一步可以证明数列{xn}所有的奇数项成等差数列,所有的偶数项也成等差数列,由等差数列的性质易得A2n-1(2n+a-2,0),A2n(2n-a,0),结合(1)的结论和三角形面积公式,即可给出S2n-1的表达式.
,进一步可以证明数列{xn}所有的奇数项成等差数列,所有的偶数项也成等差数列,由等差数列的性质易得A2n-1(2n+a-2,0),A2n(2n-a,0),结合(1)的结论和三角形面积公式,即可给出S2n-1的表达式.(3)由(2)的结论,易给出数列
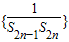 前n项和为Tn的表达式,利用裂项求和法,化简Tn的表达式再与
前n项和为Tn的表达式,利用裂项求和法,化简Tn的表达式再与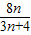 进行比较,即可得到结论.
进行比较,即可得到结论.解答:解:(1)由于点B1(1,y1),B2(2,y2),,Bn(n,yn)(n∈N*)在直线
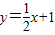 上,
上,则
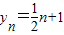 ,
,因此
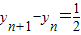 ,所以数列{yn}是等差数列;
,所以数列{yn}是等差数列;(2)由已知有
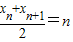 ,那么xn+xn+1=2n,同理xn+1+xn+2=2(n+1),
,那么xn+xn+1=2n,同理xn+1+xn+2=2(n+1),以上两式相减,得xn+2-xn=2,
∴x1,x3,x5,…,x2n-1,成等差数列;x2,x4,x6,…,x2n,也成等差数列,
∴x2n-1=x1+(n-1)×2=2n+a-2,x2n=x2+(n-1)×2=(2-a)+(n-1)×2=2n-a,
点A2n-1(2n+a-2,0),A2n(2n-a,0),
则|A2n-1A2n|=2(1-a),|A2nA2n+1|=2a,
而
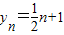 ,
,∴
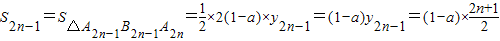 ;
;(3)由(2)得:
 ,
,则
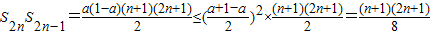
而S2nS2n-1>0,则
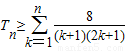 ,
,即
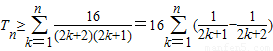
∴
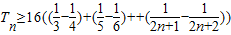
∴
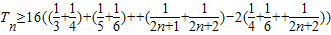
∴
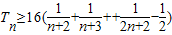
由于
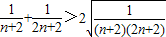 ,
,而
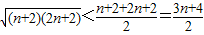 ,
,则
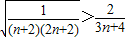 ,从而
,从而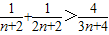 ,
,同理:

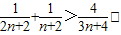
以上n+1个不等式相加得:
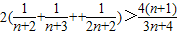
即
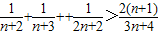 ,
,从而
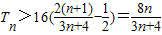 .
.点评:要判断一个数列是否为等差(比)数列,我们常用如下几种办法:①定义法,判断数列连续两项之间的差(比)是否为定值;②等差(比)中项法,判断是否每一项都是其前一项与后一项的等差(比)中项;③通项公式法,判断其通项公式是否为一次(指数)型函数;④前n项和公式法.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
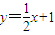 上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn,
上,点A1(x1,0),A2(x2,0),A3(x3,0),…,An(xn,0)顺次为x轴上的点,其中x1=a(0<a<1),对于任意n∈N*,点An,Bn,An+1构成以∠Bn为顶角的等腰三角形,设△AnBnAn+1的面积为Sn, 前n项和为Tn,判断Tn与
前n项和为Tn,判断Tn与 (n∈N*)的大小,并证明你的结论.
(n∈N*)的大小,并证明你的结论.