摘要：∴≤PQ＜1.-----------------------8分解二:设点P的坐标为P.如图6.作MM1⊥AB于M1.NN1⊥AB于N1. ∵△APM和△BPN是等边三角形.且都在x轴上方.∴AM =AP=x.BN=BP=2-x.∠MAP=60°.∠NBP=60°.
网址：http://m.1010jiajiao.com/timu_id_570109[举报]
在平面直角坐标系中，抛物线y=ax2+bx+3与x轴的两个交点分别为A（-3，0）、B（1，0）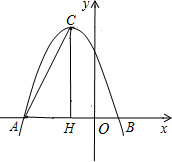
，过顶点C作CH⊥x轴于点H．
（1）直接填写：a= ，b= ，顶点C的坐标为 ；
（2）在y轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标． 查看习题详情和答案>>
，过顶点C作CH⊥x轴于点H．（1）直接填写：a=
（2）在y轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH相似时，求点P的坐标． 查看习题详情和答案>>
如图，已知⊙O的圆心O在射线PM上，PN切⊙O于Q，PO=20cm，∠P=30°，A、B两点同时从P点出发，点A以4cm/s的速度沿PM方向移动，点B沿PN方向移动，且直线AB始终垂直PN．设运动时间为t秒，求下列问题．（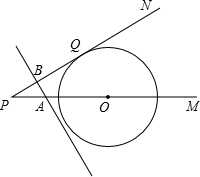
结果保留根号）
（1）求PQ的长；
（2）当t为何值时直线AB与⊙O相切？
（3）当t为何值时，直线AB与⊙O相交的弦长是16cm？ 查看习题详情和答案>>
结果保留根号）（1）求PQ的长；
（2）当t为何值时直线AB与⊙O相切？
（3）当t为何值时，直线AB与⊙O相交的弦长是16cm？ 查看习题详情和答案>>
如图，四边形ABCD和四边形ACED都是平行四边形，点R为DE的中点，BR分别交AC、CD于
点P、Q．
（1）请写出图中各对相似三角形（相似比为1除外）；
（2）求BP：PQ：QR． 查看习题详情和答案>>
点P、Q．（1）请写出图中各对相似三角形（相似比为1除外）；
（2）求BP：PQ：QR． 查看习题详情和答案>>
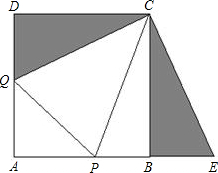如图，正方形ABCD（四个角都是直角，四条边都相等）的边长为1，AB，AD上各有一点P、Q，△APQ的周长为2，求∠PCQ．为了解决这个问题，我们在正方形外以BC和AB的延长线为边作△CBE，使得△CBE≌△CDQ．（1）△CBE可以看成是由△CDQ怎样运动变化得到的？请你描述这一运动变化；
（2）图中PQ与PE的长度是相等的．请你说明理由；
（3）请用（1）或（2）中的结论说明△PCQ≌△PCE；
（4）请用以上的结论，求∠PCQ的度数． 查看习题详情和答案>>
（1）计算：2-1+20070+
+tan45°；
（2）化简求值：(1+
)•(x2-1)，其中x=
．
（3）在数学上，对于两个数p和q有三种平均数，即算术平均数A、几何平均数G、调和平均数H，其中A=
，G=
．而调和平均数中的“调和”二字来自于音乐，毕达哥拉斯学派通过研究发现，如果三根琴弦的长度p=10，H=12，q=15满足
-
=
-
，再把它们绷得一样紧，并用同样的力弹拨，它们将会分别发出很调和的乐声．我们称p、H、q为一组调和数，而把H称为p和q的调和平均数．
①若p=2，q=6，则A= ，G= ．
②根据上述关系，用p、q的代数式表示出它们的调和平均数H；并根据你所得到的结论，再写出一组调和数． 查看习题详情和答案>>
| 1 | ||
|
（2）化简求值：(1+
| 1 |
| x-1 |
| 1 |
| 3 |
（3）在数学上，对于两个数p和q有三种平均数，即算术平均数A、几何平均数G、调和平均数H，其中A=
| p+q |
| 2 |
| pq |
| 1 |
| 10 |
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 15 |
①若p=2，q=6，则A=
②根据上述关系，用p、q的代数式表示出它们的调和平均数H；并根据你所得到的结论，再写出一组调和数． 查看习题详情和答案>>