题目内容
如图,已知⊙O的圆心O在射线PM上,PN切⊙O于Q,PO=20cm,∠P=30°,A、B两点同时从P点出发,点A以4cm/s的速度沿PM方向移动,点B沿PN方向移动,且直线AB始终垂直PN.设运动时间为t秒,求下列问题.(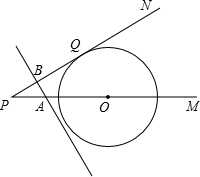 结果保留根号)
结果保留根号)(1)求PQ的长;
(2)当t为何值时直线AB与⊙O相切?
(3)当t为何值时,直线AB与⊙O相交的弦长是16cm?
分析:(1)连接OQ,由PN切⊙o于Q,根据切线的性质可得OQ⊥PN,又由PO=20cm,∠P=30°,即可求得PQ的长;
(2)作OH⊥AB于H,由AB⊥PN,即可得四边形BHOQ是矩形,当矩形BHOQ是正方形时,直线AB与⊙O相切.即可求得PA与AB的长,然后分别从当PQ-PB=OQ时,直线AB第一次与⊙O相切与当PB-PQ=OQ时,直线AB第二次与⊙O相切去分析求解,即可求得答案;
(3)由当直线AB与⊙O相交于EF时,ER=8,EO=10,即可求得OR=6,又由PB=PQ±6时,EF的长都是16cm,点A的速度是4cm/s,求得点B的速度是2
cm/s,即可求得答案.
(2)作OH⊥AB于H,由AB⊥PN,即可得四边形BHOQ是矩形,当矩形BHOQ是正方形时,直线AB与⊙O相切.即可求得PA与AB的长,然后分别从当PQ-PB=OQ时,直线AB第一次与⊙O相切与当PB-PQ=OQ时,直线AB第二次与⊙O相切去分析求解,即可求得答案;
(3)由当直线AB与⊙O相交于EF时,ER=8,EO=10,即可求得OR=6,又由PB=PQ±6时,EF的长都是16cm,点A的速度是4cm/s,求得点B的速度是2
| 3 |
解答: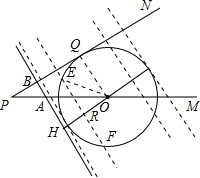 解:(1)连接OQ,
解:(1)连接OQ,
∵PN切⊙O于Q,
∴OQ⊥PN,(2分)
∵PO=20(cm),∠P=30°,
∴OQ=10(cm),PQ=10
(cm)(4分)
(2)作OH⊥AB于H,
∵AB⊥PN,
∴四边形BHOQ是矩形,
当矩形BHOQ是正方形时,直线AB与⊙O相切.
∵PA=4t,
∴AB=2t,
故PB=2
t(6分)
当PQ-PB=OQ时,直线AB第一次与⊙O相切,
∴10
-2
t=10
解得:t=5-
,
当PB-PQ=OQ时,直线AB第二次与⊙O相切,
2
t-10
=10,
解得:t=5+
,
∴当t=t=5±
时,直线AB与⊙O相切.(8分)
(3)当直线AB与⊙O相交于EF时,ER=8,EO=10,
∴OR=6,
∴PB=PQ±6时,EF的长都是16cm.(10分)
∵点A的速度是4cm/s,
∴点B的速度是2
cm/s,
∴t1=
=5-
,t2=
=5+
∴当t=5±
秒时,相交的弦长是16cm.(12分)
 解:(1)连接OQ,
解:(1)连接OQ,∵PN切⊙O于Q,
∴OQ⊥PN,(2分)
∵PO=20(cm),∠P=30°,
∴OQ=10(cm),PQ=10
| 3 |
(2)作OH⊥AB于H,
∵AB⊥PN,
∴四边形BHOQ是矩形,
当矩形BHOQ是正方形时,直线AB与⊙O相切.
∵PA=4t,
∴AB=2t,
故PB=2
| 3 |
当PQ-PB=OQ时,直线AB第一次与⊙O相切,
∴10
| 3 |
| 3 |
解得:t=5-
| 5 |
| 3 |
| 3 |
当PB-PQ=OQ时,直线AB第二次与⊙O相切,
2
| 3 |
| 3 |
解得:t=5+
| 5 |
| 3 |
| 3 |
∴当t=t=5±
| 5 |
| 3 |
| 3 |
(3)当直线AB与⊙O相交于EF时,ER=8,EO=10,
∴OR=6,
∴PB=PQ±6时,EF的长都是16cm.(10分)
∵点A的速度是4cm/s,
∴点B的速度是2
| 3 |
∴t1=
10
| ||
2
|
| 3 |
10
| ||
2
|
| 3 |
∴当t=5±
| 3 |
点评:此题考查了切线的性质,矩形的判定与性质,正方形的性质以及勾股定理等知识.此题综合性较强,难度较大,解题的关键是注意数形结合思想与方程思想的应用,注意辅助线的作法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
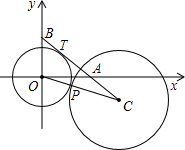 为(x,y),问N点的坐标x,y能否写成与r无关的关系式?若能,请写出关系式;若不能,请说明理由.
为(x,y),问N点的坐标x,y能否写成与r无关的关系式?若能,请写出关系式;若不能,请说明理由.

 ,
, )的切线交x轴于A点,交y轴于B点.
)的切线交x轴于A点,交y轴于B点.