摘要:例2.求证:过抛物线的焦点的弦被焦点分成的两部分线段长的倒数和为常数.并求此常数
网址:http://m.1010jiajiao.com/timu_id_569686[举报]
斜率为 的直线过抛物线
的直线过抛物线 的焦点,且与抛物线交于两点
的焦点,且与抛物线交于两点 、
、 .
.
(1)求 的值;
的值;
(2)将直线 按向量
按向量 =(-2,0)平移得直线
=(-2,0)平移得直线 ,
, 是
是 上的动点,求
上的动点,求 的最小值.
的最小值.
(3)设 (2,0),
(2,0), 为抛物线
为抛物线 上一动点,证明:存在一条定直线
上一动点,证明:存在一条定直线 ,使得
,使得 被以
被以 为直径的圆截得的弦长为定值,并求出直线
为直径的圆截得的弦长为定值,并求出直线 的方程.
的方程.
查看习题详情和答案>>
(文)斜率为1的直线过抛物线y2=4x的焦点,且与抛物线交于两点A、B.
(1)求|AB|的值;
(2)将直线AB按向量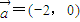 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求 的最小值.
的最小值.
(3)设C(2,0),D为抛物线y2=4x上一动点,证明:存在一条定直线l:x=a,使得l被以CD为直径的圆截得的弦长为定值,并求出直线l的方程.
查看习题详情和答案>>
(1)求|AB|的值;
(2)将直线AB按向量
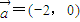 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求 的最小值.
的最小值.(3)设C(2,0),D为抛物线y2=4x上一动点,证明:存在一条定直线l:x=a,使得l被以CD为直径的圆截得的弦长为定值,并求出直线l的方程.
查看习题详情和答案>>
(文)斜率为1的直线过抛物线y2=4x的焦点,且与抛物线交于两点A、B.
(1)求|AB|的值;
(2)将直线AB按向量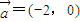 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求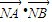 的最小值.
的最小值.
(3)设C(2,0),D为抛物线y2=4x上一动点,证明:存在一条定直线l:x=a,使得l被以CD为直径的圆截得的弦长为定值,并求出直线l的方程.
查看习题详情和答案>>
(1)求|AB|的值;
(2)将直线AB按向量
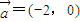 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求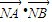 的最小值.
的最小值.(3)设C(2,0),D为抛物线y2=4x上一动点,证明:存在一条定直线l:x=a,使得l被以CD为直径的圆截得的弦长为定值,并求出直线l的方程.
查看习题详情和答案>>
 +
+ =1的中心,焦点与该椭圆的右焦点重合.
=1的中心,焦点与该椭圆的右焦点重合.