摘要：设点P是其上任意一点.焦准距为p,条件:=e

网址：http://m.1010jiajiao.com/timu_id_569678[举报]

给出4个命题：
（1）设椭圆长轴长度为2a（a＞0），椭圆上的一点P到一个焦点的距离是

a，P到一条准线的距离是

a，则此椭圆的离心率为

．
（2）若椭圆

=1（a≠b，且a，b为正的常数）的准线上任意一点到两焦点的距离分别为d₁，d₂，则|d₁²-d₂²|为定值．
（3）如果平面内动点M到定直线l的距离与M到定点F的距离之比大于1，那么动点M的轨迹是双曲线．
（4）过抛物线焦点F的直线与抛物线交于A、B两点，若A、B在抛物线准线上的射影分别为A₁、B₁，则FA₁⊥FB₁．
其中正确命题的序号依次是

．（把你认为正确的命题序号都填上）

查看习题详情和答案>>

设F₁、F₂分别是椭圆C:+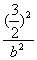=1(a＞b＞0)的左、右焦点,l为左准线,A₁、A₂分别为其长轴的左、右端点.

(1)若椭圆上的点M(1,)到F₁、F₂的距离之和为4,求椭圆方程;

(2)有一个猜想:“设P(x₁,y₁)、Q(x₂,y₂)(y₁y₂≠0)是椭圆C上的任意两点，若P、F₁、Q三点共线,则直线PA₁、QA₂、l共点.”你认为这个猜想能成立吗？请说明理由.

查看习题详情和答案>>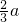

给出4个命题：
（1）设椭圆长轴长度为2a（a＞0），椭圆上的一点P到一个焦点的距离是 $数学公式$ ，P到一条准线的距离是 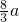$数学公式$ ，则此椭圆的离心率为 $数学公式$ ．
（2）若椭圆 $数学公式$ （a≠b，且a，b为正的常数）的准线上任意一点到两焦点的距离分别为d₁，d₂，则|d₁²-d₂²|为定值．
（3）如果平面内动点M到定直线l的距离与M到定点F的距离之比大于1，那么动点M的轨迹是双曲线．
（4）过抛物线焦点F的直线与抛物线交于A、B两点，若A、B在抛物线准线上的射影分别为A₁、B₁，则FA₁⊥FB₁．
其中正确命题的序号依次是________．（把你认为正确的命题序号都填上）

查看习题详情和答案>>

给出4个命题：
（1）设椭圆长轴长度为2a（a＞0），椭圆上的一点P到一个焦点的距离是

，P到一条准线的距离是

，则此椭圆的离心率为

．
（2）若椭圆

（a≠b，且a，b为正的常数）的准线上任意一点到两焦点的距离分别为d₁，d₂，则|d₁²-d₂²|为定值．
（3）如果平面内动点M到定直线l的距离与M到定点F的距离之比大于1，那么动点M的轨迹是双曲线．
（4）过抛物线焦点F的直线与抛物线交于A、B两点，若A、B在抛物线准线上的射影分别为A₁、B₁，则FA₁⊥FB₁．
其中正确命题的序号依次是．（把你认为正确的命题序号都填上）查看习题详情和答案>>