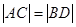摘要:由椭圆的定义可知:2a>2c.即a>c.故a2-c2>0.
网址:http://m.1010jiajiao.com/timu_id_567519[举报]
 定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:
定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:| x2 |
| 4 |
(1)若椭圆C2:
| x2 |
| 16 |
| y2 |
| 4 |
(2)写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程;若在椭圆Cb上存在两点M、N关于直线y=x+1对称,求实数b的取值范围?
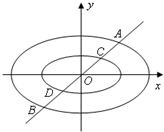
(3)如图:直线y=x与两个“相似椭圆”M:
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
 (2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:
(2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:| x2 |
| 4 |
(1)若椭圆C2:
| x2 |
| 16 |
| y2 |
| 4 |
(2)写出与椭圆C1相似且短半轴长为b的椭圆Cb的方程;若在椭圆Cb上存在两点M、N关于直线y=x+1对称,求实数b的取值范围?
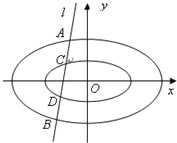
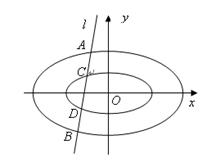
(3)如图:直线l与两个“相似椭圆”
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
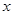 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为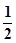 ,则m=( )
,则m=( ) B.
B.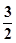 C.
C. D.
D.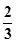
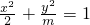 的离心率为
的离心率为 ,则实数m等于
,则实数m等于

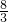

 。
。
 ,判断
,判断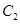 与
与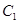 是否相似?如果相似,求出
是否相似?如果相似,求出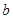 的椭圆
的椭圆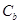 的方程;若在椭圆
的方程;若在椭圆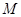 、
、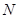 关于直线
关于直线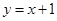 对称,求实数
对称,求实数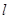 与两个“相似椭圆”
与两个“相似椭圆”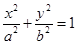 和
和 分别交于点
分别交于点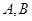 和点
和点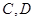 ,证明:
,证明: