摘要：例2.已知定点F和定直线l.F不在直线l上.动圆M过F且与直线l相切.求证:圆心M的轨迹是一条抛物线.解:M到l的距离为d,则MF=d, M的轨迹是一条抛物线变题:已知定点F和定圆C.F在圆C外.动圆M过F且与圆C相切.探究动圆的圆心M的轨迹是何曲线? (提示:相切须考虑外切和内切,为双曲线)思考:此处定点F也可改成定圆又如何?
网址：http://m.1010jiajiao.com/timu_id_567498[举报]
已知抛物线C1：y2=2px（p＞0）的焦点F以及椭圆C2：
+
=1，(a＞b＞0)的上、下焦点及左、右顶点均在圆O：x2+y2=1上．
（Ⅰ）求抛物线C1和椭圆C2的标准方程；
（Ⅱ）过点F的直线交抛物线C1于A、B两不同点，交y轴于点N，已知
=λ1
，
=λ2
，求证：λ1+λ2为定值．
（Ⅲ）直线l交椭圆C2于P、Q两不同点，P、Q在x轴的射影分别为P'、Q'，
•
+
•
+1=0，若点S满足：
=
+
，证明：点S在椭圆C2上．
查看习题详情和答案>>
| y2 |
| a2 |
| y2 |
| b2 |
（Ⅰ）求抛物线C1和椭圆C2的标准方程；
（Ⅱ）过点F的直线交抛物线C1于A、B两不同点，交y轴于点N，已知
| NA |
| AF |
| NB |
| BF |
（Ⅲ）直线l交椭圆C2于P、Q两不同点，P、Q在x轴的射影分别为P'、Q'，
| OP |
| OQ |
| OP′ |
| OQ′ |
| OS |
| OP |
| OQ |
已知椭圆
的离心率为
，右焦点为F（1，0），直线l经过点F且与椭圆交于A、B两点，O为坐标原点．
（1）求椭圆的方程；
（2）若P是椭圆上的一个动点，求|PO|2+|PF|2的最大值和最小值；
（3）当直线l绕点F转动时，试问：在x轴上是否存在定点S，使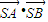
为常数，若存在，求出定点S的坐标；若不存在，请说明理由．
查看习题详情和答案>>
的离心率为，右焦点为F（1，0），直线l经过点F且与椭圆交于A、B两点，O为坐标原点．（1）求椭圆的方程；
（2）若P是椭圆上的一个动点，求|PO|2+|PF|2的最大值和最小值；
（3）当直线l绕点F转动时，试问：在x轴上是否存在定点S，使
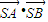为常数，若存在，求出定点S的坐标；若不存在，请说明理由．
查看习题详情和答案>>
（2012•兰州模拟）已知点M是直线x=-
上的动点，F(
，0)为定点，过点M且垂直于直线x=-
的直线和线段MF的垂直平分线相交于点P．
（1）求点P的轨迹方程；
（2）经过点Q（a，0）（a＞0）且与x轴不垂直的直线l与点P的轨迹有两个不同交点A、B，若在x轴上存在点C，使得△ABC为正三角形，求实数a的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
（1）求点P的轨迹方程；
（2）经过点Q（a，0）（a＞0）且与x轴不垂直的直线l与点P的轨迹有两个不同交点A、B，若在x轴上存在点C，使得△ABC为正三角形，求实数a的取值范围．