网址:http://m.1010jiajiao.com/timu_id_566579[举报]
一.BCAAC DAAAC
二.11.5 12.0 13.(4,12)14.[-3,0)∪(3,+∞) 15①②③
三.16解:(1)由正弦定理有: ;。。。。。(2分)
;。。。。。(2分)
∴ ,
, ;。。。。。。。。。。。。。(4分)
;。。。。。。。。。。。。。(4分)
∴


 。。。。。。。。。。。。。。。。。。。(7分)
。。。。。。。。。。。。。。。。。。。(7分)
(2)由 ;。。。。。。。。。。。。。。。。。。。。。。(8分)
;。。。。。。。。。。。。。。。。。。。。。。(8分)
∴ ;。。。。。。。。(10分)∴
;。。。。。。。。(10分)∴
 。。。。。。。。。。。。。(12分)
。。。。。。。。。。。。。(12分)
17。解:(Ⅰ)由题意可知
 数列
数列 是等差数列 ………(2分)
是等差数列 ………(2分)
 ,
,

当 时,
时,
两式相减,得 ………………………(4分)
………………………(4分)
 时也成立
时也成立
∴ 的通项公式为:
的通项公式为: ………………………………(6分)
………………………………(6分)
(Ⅱ)由前 项和公式得
项和公式得
当 时,
时, ………………………………………(8分)
………………………………………(8分)
∵ 最大, 则有
最大, 则有 ,解得
,解得 …………………………….(12分)
…………………………….(12分)
18。解:(Ⅰ)当 时,
时, ,
, .
.

 .
……………………………………… 2分
.
……………………………………… 2分
∵  ,
,
∴  解得
解得  或
或 .
.
∴ 当 时,使不等式
时,使不等式 成立的x的取值范围是
成立的x的取值范围是
 .…………………………………………… 5分
.…………………………………………… 5分
(Ⅱ)∵  ,…… 8分
,…… 8分
∴ 当m<0时, ;
;
当m=0时,  ;
;
当 时,
时, ;
;
当m=1时, ;
;
当m>1时, .
.............................................12
.
.............................................12
19。解:设对甲厂投入x万元(0≤x≤c),则对乙厂投入为c―x万元.所得利润为
y=x+40 (0≤x≤c) ……………………(3分)
(0≤x≤c) ……………………(3分)
令 =t(0≤t≤
=t(0≤t≤ ),则x=c-t2
),则x=c-t2
∴y=f(t)=-t2+40t+c=-(t―20)2+c+400……………………(6分)
当 ≥20,即c≥400时,则t=20, 即x=c―400时, ymax =c+400… (8分)
≥20,即c≥400时,则t=20, 即x=c―400时, ymax =c+400… (8分)
当0< <20,
即0<c<400时,则t=
<20,
即0<c<400时,则t= ,即x=0时,ymax=40
,即x=0时,ymax=40  .…(10分)
.…(10分)
答:若政府投资c不少于400万元时,应对甲投入c―400万元, 乙对投入400万元,可获得最大利润c+400万元.政府投资c小于400万元时,应对甲不投入,的把全部资金c都投入乙商品可获得最大利润40 万元.…(12分)
万元.…(12分)
20。解:(1)设C:+=1(a>b>0),设c>0,c2=a2-b2,由条件知a-c=,=,
∴a=1,b=c=,
故C的方程为:y2+=1 ………………………………………(5分)
(2)由=λ得-=λ(-),(1+λ)=+λ,
∴λ+1=4,λ=3 ………………………………………………(7分)
设l与椭圆C交点为A(x1,y1),B(x2,y2)
得(k2+2)x2+2kmx+(m2-1)=0
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0 (*)
x1+x2=, x1x2= ………………………………………………(9分)
∵=3 ∴-x1=3x2 ∴
消去x2,得3(x1+x2)2+4x1x2=0,∴3()2+4=0
整理得4k2m2+2m2-k2-2=0 ………………………………………………(11)分
m2=时,上式不成立;m2≠时,k2=,
因λ=3 ∴k≠0 ∴k2=>0,∴-1<m<- 或 <m<1
容易验证k2>2m2-2成立,所以(*)成立
即所求m的取值范围为(-1,-)∪(,1) ………………………(13分)
21. 解:(Ⅰ)易知0是f(x)-x=0的根………………………(1分)
0< ≤
≤ (x)=
(x)= +
+ sinx≤
sinx≤ <1………..(3分)
<1………..(3分)
∴f(x)∈M…………………………………………………(4分)
Ⅱ)假设 存在两个实根
存在两个实根 ,则
,则 ,
, 不妨设
不妨设 ,由题知存在实数
,由题知存在实数 ,使得
,使得 成立。∵
成立。∵ ,
, 且
且 ,∴
,∴
与已知矛盾,所以方程 只有一个实数根……………………(8分)
只有一个实数根……………………(8分)
(Ⅲ) 不妨设 ,∵
,∵ ,∴
,∴ 为增函数,∴
为增函数,∴ ,又∵
,又∵ ∴函数
∴函数 为减函数,∴
为减函数,∴ ,………………….(10分)
,………………….(10分)
∴ ,即
,即 ,……..(12分)
,……..(12分)
∴ ….(14分)
….(14分)
| 1 |
| 4 |
(1)过点,A(p0,
| 1 |
| 4 |
| |p0| |
| 2 |
(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠0.过M(a,b)作L的两条切线l1,l2,切点分别为E(p1,
| 1 |
| 4 |
| p | 2 1 |
| 1 |
| 4 |
| |p1| |
| 2 |
(3)设D={ (x,y)|y≤x-1,y≥
| 1 |
| 4 |
| 5 |
| 4 |
在平面直角坐标系xoy上,给定抛物线L:y= x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
(1)过点,A(p0, p02)(p0≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)=
p02)(p0≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)=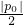 ;
;
(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠0.过M(a,b)作L的两条切线l1,l2,切点分别为E(p1, ),E′(p2,
),E′(p2, p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=
p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=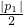 .
.
(3)设D={ (x,y)|y≤x-1,y≥ (x+1)2-
(x+1)2- }.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
}.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
查看习题详情和答案>>
| 1 |
| 4 |
(1)过点,A(p0,
| 1 |
| 4 |
| |p0| |
| 2 |
(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠0.过M(a,b)作L的两条切线l1,l2,切点分别为E(p1,
| 1 |
| 4 |
| p | 21 |
| 1 |
| 4 |
| |p1| |
| 2 |
(3)设D={ (x,y)|y≤x-1,y≥
| 1 |
| 4 |
| 5 |
| 4 |
 x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.(1)过点A(p0,
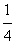 p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=
p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)= ;
;(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠0。过M(a,b)作L的两条切线l1,l2,切点分别为E(p1,
 p12),E′(p2,
p12),E′(p2, p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X
p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X |P1|>|P2|
|P1|>|P2| φ(a,b)=
φ(a,b)=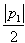 ;
;(3)设D={(x,y)|y≤x-1,y≥
 (x+1)2-
(x+1)2- },当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。
},当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。 x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2.实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.(1)过点,A(p,
 p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)=
p2)(p≠0),作L的切线交y轴于点B.证明:对线段AB上的任一点Q(p,q),有φ(p,q)= ;
;(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠0.过M(a,b)作L的两条切线l1,l2,切点分别为E(p1,
 ),E′(p2,
),E′(p2, p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)=
p22),l1,l2与y轴分别交于F,F′.线段EF上异于两端点的点集记为X.证明:M(a,b)∈X?|P1|<|P2|?φ(a,b)= .
.(3)设D={ (x,y)|y≤x-1,y≥
 (x+1)2-
(x+1)2- }.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)
}.当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)查看习题详情和答案>>