题目内容
在平面直角坐标系xOy上,给定抛物线L:y=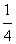 x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
(1)过点A(p0,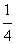 p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=
p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=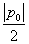 ;
;
(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠0。过M(a,b)作L的两条切线l1,l2,切点分别为E(p1,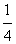 p12),E′(p2,
p12),E′(p2,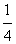 p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X
p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X |P1|>|P2|
|P1|>|P2| φ(a,b)=
φ(a,b)=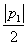 ;
;
(3)设D={(x,y)|y≤x-1,y≥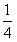 (x+1)2-
(x+1)2-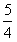 },当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。
},当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。
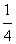 x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.
x2,实数p,q满足p2-4q≥0,x1,x2是方程x2-px+q=0的两根,记φ(p,q)=max{|x1|,|x2|}.(1)过点A(p0,
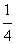 p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=
p0)(p0≠0)作L的切线教y轴于点B。证明:对线段AB上任一点Q(p,q)有φ(p,q)=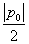 ;
;(2)设M(a,b)是定点,其中a,b满足a2-4b>0,a≠0。过M(a,b)作L的两条切线l1,l2,切点分别为E(p1,
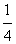 p12),E′(p2,
p12),E′(p2,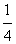 p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X
p22),l1,l2与y轴分别交与F,F'。线段EF上异于两端点的点集记为X。证明:M(a,b)∈X |P1|>|P2|
|P1|>|P2| φ(a,b)=
φ(a,b)= ;
;(3)设D={(x,y)|y≤x-1,y≥
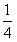 (x+1)2-
(x+1)2-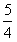 },当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。
},当点(p,q)取遍D时,求φ(p,q)的最小值 (记为φmin)和最大值(记为φmax)。解:(1)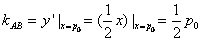
直线AB方程为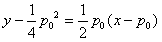 ,即
,即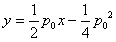
∴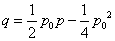
方程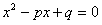 的判别式
的判别式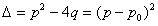
两根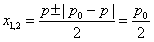 或
或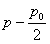
∵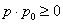
∴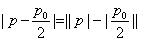
又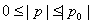
∴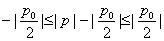
得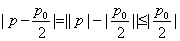
∴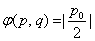 。
。
(2)由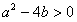 知点
知点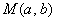 在抛物线L的下方
在抛物线L的下方
①当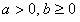 时,作图可知,若
时,作图可知,若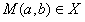 ,则
,则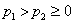 ,得
,得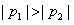
若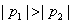 ,显然有点
,显然有点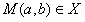
∴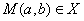
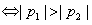
②当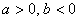 时,点
时,点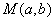 在第二象限,作图可知,若
在第二象限,作图可知,若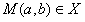 ,则
,则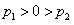 ,且
,且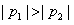
若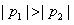 ,显然有点
,显然有点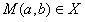
∴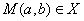
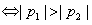
根据曲线的对称性可知,当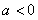 时,
时,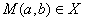
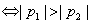
综上所述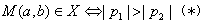
由(1)知点M在直线EF上,方程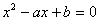 的两根
的两根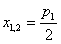 或
或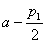
同理点M在直线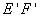 上,方程
上,方程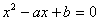 的两根
的两根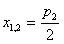 或
或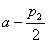
若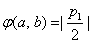 ,则
,则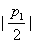 不比
不比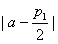 ,
,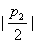 ,
,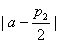 小
小
∴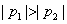
又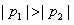
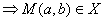
∴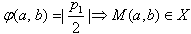
又由(1)知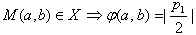
∴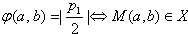
综合(*)式,得证。
(3)联立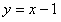 ,
,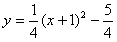 得交点
得交点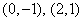 ,可知
,可知
过点作抛物线L的切线,设切点为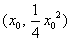 ,则
,则
得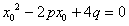 ,解得
,解得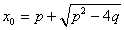
又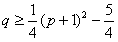 ,即
,即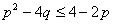
∴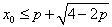
设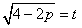
∴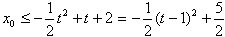
∵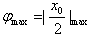
又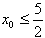
∴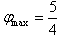
∵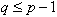
∴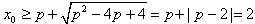
∴ 。
。
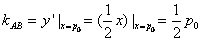
直线AB方程为
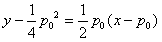 ,即
,即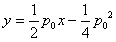
∴
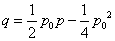
方程
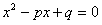 的判别式
的判别式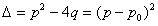
两根
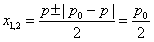 或
或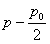
∵
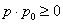
∴
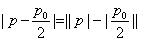
又
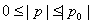
∴
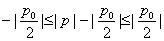
得
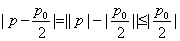
∴
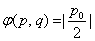 。
。(2)由
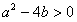 知点
知点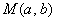 在抛物线L的下方
在抛物线L的下方①当
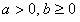 时,作图可知,若
时,作图可知,若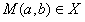 ,则
,则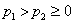 ,得
,得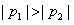
若
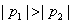 ,显然有点
,显然有点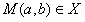
∴
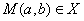
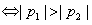
②当
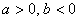 时,点
时,点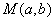 在第二象限,作图可知,若
在第二象限,作图可知,若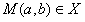 ,则
,则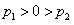 ,且
,且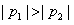
若
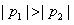 ,显然有点
,显然有点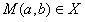
∴
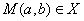
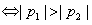
根据曲线的对称性可知,当
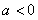 时,
时,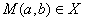
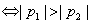
综上所述
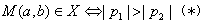
由(1)知点M在直线EF上,方程
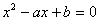 的两根
的两根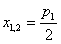 或
或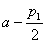
同理点M在直线
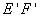 上,方程
上,方程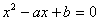 的两根
的两根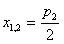 或
或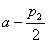
若
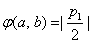 ,则
,则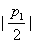 不比
不比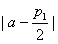 ,
,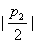 ,
,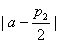 小
小∴
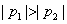
又
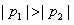
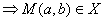
∴
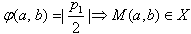
又由(1)知
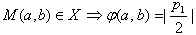
∴
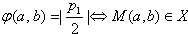
综合(*)式,得证。
(3)联立
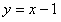 ,
,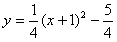 得交点
得交点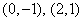 ,可知
,可知
过点作抛物线L的切线,设切点为
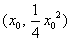 ,则
,则
得
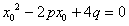 ,解得
,解得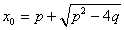
又
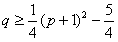 ,即
,即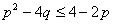
∴
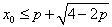
设
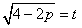
∴
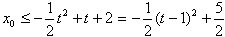
∵
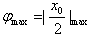
又
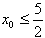
∴
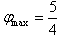
∵
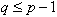
∴
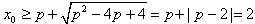
∴
 。
。
练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.