网址:http://m.1010jiajiao.com/timu_id_5631[举报]
一、选择题
1.B 2.C 3.C 4.C 5.D 6.A 7.D 8.A
二、填空题
9.-8 10.(-1,-2) 11. 12.(2分);2(3分)
13.(3分) 14.3.5
三、解答题
15.解:(Ⅰ)由已知得 ………………2分
………………4分
在三角形ABC中,C=60° ………………6分
(Ⅱ)∵ …………8分
又∵ ………………9分
∴
∴ ………………11分
∴
∴ ………………13分(少一组值扣1分)
16.[解法一](Ⅰ)证:在直三棱柱ABC―A1B1C1中,AC//A1C1 ………………2分
又平面ACD ∴A1C1//平面ACD ………………4分
(Ⅱ)在直三棱柱ABC―A1B1C1中,A1A⊥平面ABC
∴A1A⊥AC ………………6分 又∠BAC=90° ∴AC⊥AB
∴AC⊥平面A1ABB1 ………………8分
又A1D平面A1ABB1, ∴AC⊥A1D
∴异面直线AC与A1D所成的角大小为 ………………9分
(Ⅲ)∵△A1B1D和△ABD都为等腰直角三角形,∴∠A1DB1=∠ADB=45°
∴∠A1DA=90°即 A1D⊥AD …………11分 由(Ⅱ)知A1D⊥AC,
∴A1D⊥平面ACD ……………………14分
[解法二]向量法(略)
17.解:(Ⅰ)圆心坐标C(-1,2),半径。 ………………3分(圆心横纵坐标及半径各1分)
(Ⅱ)∵切线在两坐标轴上的截距相等且不为零,
设直线方程 ………………4分
∵圆C:
∴圆心C(-1,2)到切线的距离等于圆半径,
即: ………………6分
∴a=-1或a=3,
所求切线方程为:
(Ⅲ)∵切线PM与半径CM垂直,设P(x,y)
∴|PM|2=|PC|2-|CM|2 ………………10分
∴ ………………11分
所以点P的轨迹方程为 ………………13分
18.(Ⅰ)证明:∵
……………………1分
……………………3分
∴数列{bn}是首项为2,公比为2的等比数列。 ………………4分
(Ⅱ)解: ………………5分
由(Ⅰ)得 …………7分
∴ ………………8分
(Ⅲ)由(Ⅱ)可得 ………………9分
利用错位相减法可得, ………………14分
19.解:(Ⅰ)由已知得 ………………2分
又
可得 ………………4分
又
即
(0,x1)
x1
(x1,x2)
x2
(x2,2)
+
0
-
0
+
ㄊ
极大值
ㄋ
极小值
ㄊ
所以为的极大值,为的极小值.……6分
(Ⅱ)由(Ⅰ)
…………9分
……12分
……13分
20.解:(Ⅰ)由题意知
则双曲线方程为:……3分
(Ⅱ)设
设PQ方程为:代入双曲线方程可得:
由于P、Q都在双曲线的右支上,所以,
……4分
……5分
由于
由……6分
……7分
此时
……8分
(Ⅲ)存在实数,满足题设条件
……9分
把(3)(4)代入(2)得:……(5)
由(1)(5)得:……11分
,满足题设条件. ………………13分
(本小题满分13分)
已知直线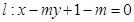
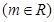 ,圆
,圆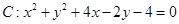 .
.
(Ⅰ)证明:对任意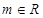 ,直线
,直线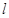 恒过一定点N,且直线
恒过一定点N,且直线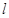 与圆C恒有两个公共点;
与圆C恒有两个公共点;
(Ⅱ)设以CN为直径的圆为圆D(D为CN中点),求证圆D的方程为: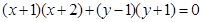
(Ⅲ)设直线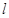 与圆
与圆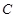 的交于A、B两点,与圆D:
的交于A、B两点,与圆D: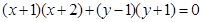 交于点
交于点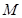 (异于C、N),当
(异于C、N),当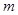 变化时,求证
变化时,求证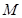 为AB的中点.
为AB的中点.
(本小题满分13分)
已知直线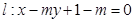
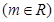 ,圆
,圆 .
.
(Ⅰ)证明:对任意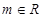 ,直线
,直线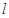 恒过一定点N,且直线
恒过一定点N,且直线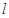 与圆C恒有两个公共点;
与圆C恒有两个公共点;
(Ⅱ)设以CN为直径的圆为圆D(D为CN中点),求证圆D的方程为: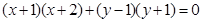
(Ⅲ)设直线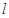 与圆
与圆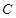 的交于A、B两点,与圆D:
的交于A、B两点,与圆D: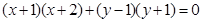 交于点
交于点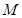 (异于C、N),当
(异于C、N),当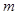 变化时,求证
变化时,求证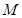 为AB的中点.
为AB的中点.
查看习题详情和答案>>
(本小题满分13分)
已知m,n表示先后抛掷一个骰子所得到正面向上的点数,方程C: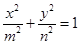
(1)求共可以组成多少个不同的方程C;
(2)求能组成落在区域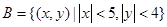 且焦点在X轴的椭圆的概率;
且焦点在X轴的椭圆的概率;
(3)在已知方程C为落在区域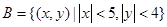 且焦点在X轴的椭圆的情况下,求离心率为
且焦点在X轴的椭圆的情况下,求离心率为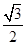 的概率
的概率
查看习题详情和答案>>

 ,圆
,圆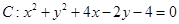 .
. ,直线
,直线 恒过一定点N,且直线
恒过一定点N,且直线
 的交于A、B两点,与圆D:
的交于A、B两点,与圆D: (异于C、N),当
(异于C、N),当 变化时,求证
变化时,求证