网址:http://m.1010jiajiao.com/timu_id_558520[举报]
一、选择题:本大题共12小题,每小题5分,共60分。
ABBD DABD BCCA
二、填空题:本大题共4小题,每小题4分,共16分。
13. 14.3 15.
14.3 15. 16.①③
16.①③
三、解答题:本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。
17.解:(I) ………2分
………2分
依题意函数
所以 …………4分
…………4分

(II)

18.解:(I)由题意得:上年度的利润的 万元;
万元;
本年度每辆车的投入成本为 万元;
万元;
本年度每辆车的出厂价为 万元;
万元;
本年度年销售量为 ………………2分
………………2分
因此本年度的利润为

(II)本年度的利润为

………………7分
则
由 (舍去)。 …………9分
(舍去)。 …………9分
|


 平面BCE,BP
平面BCE,BP 平面BCE,
平面BCE, ………………9分
………………9分 ……10分
……10分 为平面ACD的法向量。
为平面ACD的法向量。
 ,即平面BCE与平面ACD所成锐二面角为45°。…………12分
,即平面BCE与平面ACD所成锐二面角为45°。…………12分 ,
, , …………3分
, …………3分 , …………5分
, …………5分 的等比数列。 …………6分
的等比数列。 …………6分 …………7分
…………7分



 于D、E两点,并以线段DE为直径的圆都过原点。设
于D、E两点,并以线段DE为直径的圆都过原点。设

 …………7分
…………7分



 …………1分
…………1分 …………2分
…………2分








 ;
; …………5分
…………5分
 ,
, ,故不成立。 …………7分
,故不成立。 …………7分 由(I)知
由(I)知 ,且是极大值,同时也是最大值。
,且是极大值,同时也是最大值。
 …………10分
…………10分

 是两个不同的平面,m,n是两条不同的直线,给出下列命题:( )
是两个不同的平面,m,n是两条不同的直线,给出下列命题:( ) ;
;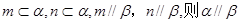 ;
;  是异面直线,那么
是异面直线,那么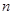 与
与 相交;
相交;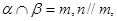 且
且 ,则
,则 且
且 其中正确的命题是( )
其中正确的命题是( )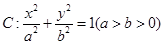 的焦点和上顶点分别为
的焦点和上顶点分别为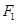 、
、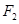 、
、 ,我们称
,我们称 为椭圆
为椭圆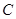 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.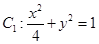 和
和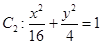 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出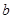 的椭圆为
的椭圆为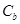 ,且直线
,且直线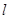 与椭圆为
与椭圆为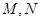 (异于端点),试问:当
(异于端点),试问:当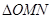 面积最大时,
面积最大时,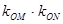 是否与
是否与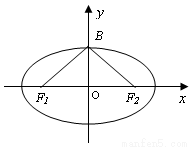
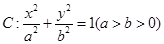 的焦点和上顶点分别为
的焦点和上顶点分别为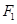 、
、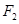 、
、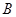 ,我们称
,我们称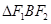 为椭圆
为椭圆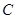 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 ,判断
,判断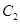 与
与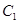 是否相似,如果相似则求出
是否相似,如果相似则求出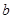 的椭圆为
的椭圆为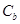 ,且直线
,且直线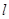 与椭圆为
与椭圆为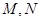 (异于端点),试问:当
(异于端点),试问:当 面积最大时,
面积最大时,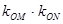 是否与
是否与