摘要：定义在R上的函数的导数.其中常数.则函数

网址：http://m.1010jiajiao.com/timu_id_548489[举报]

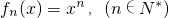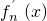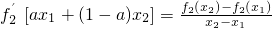已知定义在实数集上的函数 $数学公式$ ，其导函数记为 $数学公式$ ，且满足 $数学公式$ ，其中a、x₁、x₂为常数，x₁≠x₂．设函数g（x）=f₁（x）+mf₂（x）-lnf₃（x），（m∈R且m≠0）．
（Ⅰ）求实数a的值；
（Ⅱ）若m=1，求函数g（x）的单调区间；
（Ⅲ）求函数g（x）在x∈[0，a]的图象上任一点处的切线斜率k的最大值．

查看习题详情和答案>>

已知定义在实数集上的函数

，其导函数记为

，其中a、x₁、x₂为常数，x₁≠x₂．设函数g（x）=f₁（x）+mf₂（x）-lnf₃（x），（m∈R且m≠0）．
（Ⅰ）求实数a的值；
（Ⅱ）若m=1，求函数g（x）的单调区间；
（Ⅲ）求函数g（x）在x∈[0，a]的图象上任一点处的切线斜率k的最大值．
查看习题详情和答案>>

15、已知函数f（x）是定义在实数集R上的函数，给出下列结论：
①若存在常数x₀，使f′（x）=0，则函数f（x）必在x₀处取得极值；
②若函数f（x）在x₀处取得极值，则函数f（x）在x₀处必可导；
③若函数f（x）在R上处处可导，则它有极小值就是它在R上的最小值；
④若对于任意x≠x₀都有f（x）＞f（x₀），则f（x₀）是函数f（x）的最小值；
⑤若对于任意x＜x₀有f′（x）＞0，对于任意x＞x₀有f′（x）＜0，则f（x₀）是函数f（x）的一个最大值；
其中正确结论的序号是

查看习题详情和答案>>

已知函数f（x）是定义在实数集R上的函数，给出下列结论：
①若存在常数x₀，使f′（x）=0，则函数f（x）必在x₀处取得极值；
②若函数f（x）在x₀处取得极值，则函数f（x）在x₀处必可导；
③若函数f（x）在R上处处可导，则它有极小值就是它在R上的最小值；
④若对于任意x≠x₀都有f（x）＞f（x₀），则f（x₀）是函数f（x）的最小值；
⑤若对于任意x＜x₀有f′（x）＞0，对于任意x＞x₀有f′（x）＜0，则f（x₀）是函数f（x）的一个最大值；
其中正确结论的序号是 ______．

查看习题详情和答案>>

已知函数f（x）是定义在实数集R上的函数，给出下列结论：
①若存在常数x，使f′（x）=0，则函数f（x）必在x处取得极值；
②若函数f（x）在x处取得极值，则函数f（x）在x处必可导；
③若函数f（x）在R上处处可导，则它有极小值就是它在R上的最小值；
④若对于任意x≠x都有f（x）＞f（x），则f（x）是函数f（x）的最小值；
⑤若对于任意x＜x有f′（x）＞0，对于任意x＞x有f′（x）＜0，则f（x）是函数f（x）的一个最大值；
其中正确结论的序号是．查看习题详情和答案>>