摘要:解 (Ⅰ)由题意知
网址:http://m.1010jiajiao.com/timu_id_54701[举报]
(2009•金山区二模)设函数f(x)=x2+x.(1)解不等式:f(x)<0;(2)请先阅读下列材料,然后回答问题.
材料:已知函数g(x)=-
,问函数g(x)是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,说明理由.一个同学给出了如下解答:
解:令u=-f(x)=-x2-x,则u=-(x+
)2+
,
当x=-
时,u有最大值,umax=
,显然u没有最小值,
∴当x=-
时,g(x)有最小值4,没有最大值.
请回答:上述解答是否正确?若不正确,请给出正确的解答;
(3)设an=
,请提出此问题的一个结论,例如:求通项an.并给出正确解答.
注意:第(3)题中所提问题单独给分,.解答也单独给分.本题按照所提问题的难度分层给分,解答也相应给分,如果同时提出两个问题,则就高不就低,解答也相同处理.
查看习题详情和答案>>
材料:已知函数g(x)=-
| 1 |
| f(x) |
解:令u=-f(x)=-x2-x,则u=-(x+
| 1 |
| 2 |
| 1 |
| 4 |
当x=-
| 1 |
| 2 |
| 1 |
| 4 |
∴当x=-
| 1 |
| 2 |
请回答:上述解答是否正确?若不正确,请给出正确的解答;
(3)设an=
| f(n) |
| 2n-1 |
注意:第(3)题中所提问题单独给分,.解答也单独给分.本题按照所提问题的难度分层给分,解答也相应给分,如果同时提出两个问题,则就高不就低,解答也相同处理.
(本题满分12分)
设二次函数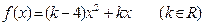 ,对任意实数
,对任意实数 ,有
,有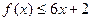 恒成立;数列
恒成立;数列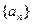 满足
满足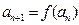 .
.
(1)求函数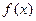 的解析式;
的解析式;
(2)试写出一个区间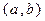 ,使得当
,使得当 时,
时,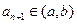 且数列
且数列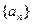 是递增数列,并说明理由;
是递增数列,并说明理由;
(3)已知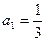 ,是否存在非零整数
,是否存在非零整数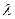 ,使得对任意
,使得对任意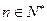 ,都有
,都有
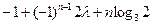 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.
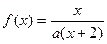 ,方程
,方程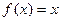 有唯一解,已知
有唯一解,已知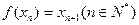 ,且
,且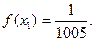
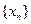 的通项公式;
的通项公式;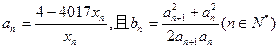 ,求和
,求和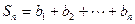 ;
;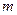 ,使得对任意
,使得对任意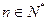 ,有
,有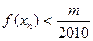 成立,若存在;求出
成立,若存在;求出 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数. ,总有
,总有 ;
; 时,总有
时,总有 成立.
成立. 与
与 是定义在
是定义在 是否为
是否为 函数?并说明理由;
函数?并说明理由; 是
是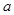 的值;
的值; ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 ,对任意实数
,对任意实数 ,有
,有 恒成立;数列
恒成立;数列 满足
满足 .
. 的解析式;
的解析式; ,使得当
,使得当 时,
时, 且数列
且数列 ,是否存在非零整数
,是否存在非零整数 ,使得对任意
,使得对任意 ,都有
,都有
 恒成立,若存在,求之;若不存在,说明理由.
恒成立,若存在,求之;若不存在,说明理由.