摘要：当时.的极大值为.没有极小值
网址：http://m.1010jiajiao.com/timu_id_544319[举报]
已知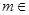
R，函数
．
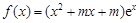⑴若函数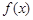
没有零点，求实数
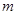的取值范围；
⑵若函数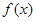
存在极大值，并记为
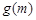，求
的表达式；
⑶当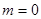
时，求证：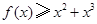
．
【解析】(1)求导研究函数f(x)的最值，说明函数f(x)的最大值<0,或f(x)的最小值>0.
(2)根据第（1）问的求解过程，直接得到g(m).
（3）构造函数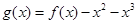
,证明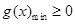
即可，然后利用导数求g(x)的最小值.
查看习题详情和答案>>
设函数y=f（x）在（a，b）上的导函数为f′（x），f′（x）在（a，b）上的导函数为f″（x），若在a，b）上，f″（x）＜0恒成立，则称函数函数f（x）在（a，b）上为“凸函数”．已知当m≤2时，f(x)=
x3-
mx2+x在（-1，2）上是“凸函数”．则f（x）在（-1，2）上（ ）
| 1 |
| 6 |
| 1 |
| 2 |
| A、既有极大值，也有极小值 |
| B、既有极大值，也有最小值 |
| C、有极大值，没有极小值 |
| D、没有极大值，也没有极小值 |
设函数y=f（x）在（a，b）上的导函数为f′（x），f′（x）在（a，b）上的导函数为f″（x），若在a，b）上，f″（x）＜0恒成立，则称函数函数f（x）在（a，b）上为“凸函数”．已知当m≤2时，f(x)=
x3-
mx2+x在（-1，2）上是“凸函数”．则f（x）在（-1，2）上（ ）
查看习题详情和答案>>
| 1 |
| 6 |
| 1 |
| 2 |
| A．既有极大值，也有极小值 |
| B．既有极大值，也有最小值 |
| C．有极大值，没有极小值 |
| D．没有极大值，也没有极小值 |
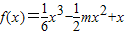在（-1，2）上是“凸函数”．则f（x）在（-1，2）上（ ）
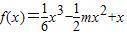在（-1，2）上是“凸函数”．则f（x）在（-1，2）上（ ）