.化为直角坐标方程得,——青夏教育精英家教网—

摘要：.化为直角坐标方程得,

网址：http://m.1010jiajiao.com/timu_id_543447[举报]

．
（1）求圆C₁的方程；
（2）设圆C₁和x轴相交于A、B两点，点P为圆C₁上不同于A、B的任意一点，直线PA、PB交y轴于M、N点．当点P变化时，以MN为直径的圆C₂是否经过圆C₁内一定点？请证明你的结论；
（3）若△RST的顶点R在直线x=-1上，S、T在圆C₁上，且直线RS过圆心C₁，∠SRT=30°，求点R的纵坐标的范围．查看习题详情和答案>>

在平面直角坐标系xoy中，曲线C₁的参数方程为

x=4cosθ

y=2sinθ

（θ为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，得曲线C₂的极坐标方程为ρ=2cosθ-4sinθ（ρ＞0）．
（Ⅰ）化曲线C₁、C₂的方程为普通方程，并说明它们分别表示什么曲线；
（Ⅱ）设曲线C₁与x轴的一个交点的坐标为P（m，0）（m＞0），经过点P作曲线C₂的切线l，求切线l的方程．查看习题详情和答案>>

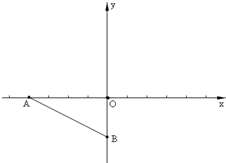在平面直角坐标系xOy中，已知定点A（-4，0），B（0，-2），半径为r的圆M的圆心M在线段AB的垂直平分线上，且在y轴右侧，圆M被y轴截得的弦长为

r．
（1）若r为正常数，求圆M的方程；
（2）当r变化时，是否存在定直线l与圆相切？如果存在求出定直线l的方程；如果不存在，请说明理由．

查看习题详情和答案>>

在平面直角坐标系xoy中，已知定点A（-4，0），B（4，0），动点P与A、B连线低斜率之积为。

（1）求点P的轨迹方程；

（2）设点P的轨迹与y轴负半轴交于点C，半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得弦长为。

（Ⅰ）求圆M的方程；

（Ⅱ）当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如

果不存在，说明理由。

查看习题详情和答案>>

在平面直角坐标系xOy中，已知定点A(－4，0)、B(4，0)，动点P与A、B连线的斜率之积为－.
(1)求点P的轨迹方程；
(2)设点P的轨迹与y轴负半轴交于点C.半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得的弦长为r.
(ⅰ)求圆M的方程；
(ⅱ)当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如果不存在，说明理由．

查看习题详情和答案>>

试题分类