已知函数f(x)=e^x-ax，其中a＞0.

（1）若对一切x∈R，f(x) 1恒成立，求a的取值集合；

（2)在函数f(x)的图像上去定点A（x₁, f(x₁)）,B(x₂, f(x₂))(x₁<x₂)，记直线AB的斜率为k，证明：存在x₀∈（x₁,x₂）,使恒成立.

【解析】解：令.

当时单调递减；当时单调递增，故当时，取最小值

于是对一切恒成立，当且仅当.　　　　　　　　①

令则

当时，单调递增；当时，单调递减.

故当时，取最大值.因此，当且仅当时，①式成立.

综上所述，的取值集合为.

（Ⅱ）由题意知，令则

令，则.当时，单调递减；当时，单调递增.故当，即

从而，又

所以因为函数在区间上的图像是连续不断的一条曲线，所以存在使即成立.

【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等，考查运算能力，考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出取最小值对一切x∈R，f(x) 1恒成立转化为从而得出求a的取值集合；第二问在假设存在的情况下进行推理，然后把问题归结为一个方程是否存在解的问题，通过构造函数，研究这个函数的性质进行分析判断.

某省环保研究所对市中心每天环境放射性污染情况进行调查研究后，发现一天中环境综合放射性污染指数与时刻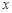(时) 的关系为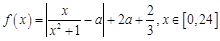，其中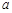是与气象有关的参数，且．

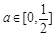（1）令, 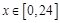，写出该函数的单调区间，并选择其中一种情形进行证明；

（2）若用每天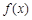的最大值作为当天的综合放射性污染指数，并记作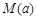，求；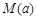

（3）省政府规定，每天的综合放射性污染指数不得超过2，试问目前市中心的综合放射性污染指数是否超标？

【解析】第一问利用定义法求证单调性，并判定结论。

第二问（2）由函数的单调性知，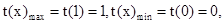

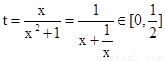∴，即t的取值范围是． 

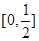当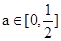时，记

则 

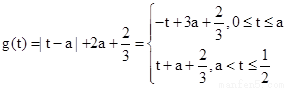
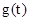∵在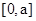上单调递减，在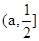上单调递增，

第三问因为当且仅当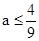时，.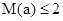

故当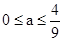时不超标，当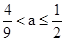时超标．