摘要:(Ⅰ).令得-----2分
网址:http://m.1010jiajiao.com/timu_id_542038[举报]
(2009福建卷理)(本小题满分14分)
已知函数![]() ,且
,且![]()
![]()
![]()
(1) 试用含![]() 的代数式表示b,并求
的代数式表示b,并求![]() 的单调区间;
的单调区间;
(2)令![]() ,设函数
,设函数![]() 在
在![]() 处取得极值,记点M (
处取得极值,记点M (![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),P(
),P(![]() ),
), ![]() ,请仔细观察曲线
,请仔细观察曲线![]() 在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
在点P处的切线与线段MP的位置变化趋势,并解释以下问题:
(I)若对任意的m ![]() (
(![]() , x
, x![]() ),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
),线段MP与曲线f(x)均有异于M,P的公共点,试确定t的最小值,并证明你的结论;
(本小题满分14分)
已知函数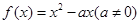 ,
,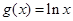 ,
,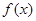 图象与
图象与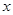 轴异于原点的交点M处的切线为
轴异于原点的交点M处的切线为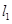 ,
,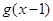 与
与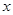 轴的交点N处的切线为
轴的交点N处的切线为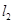 , 并且
, 并且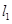 与
与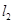 平行.
平行.
(1)求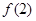 的值;
的值;
(2)已知实数t∈R,求函数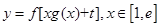 的最小值;
的最小值;
(3)令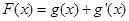 ,给定
,给定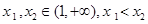 ,对于两个大于1的正数
,对于两个大于1的正数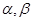 ,
,
存在实数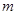 满足:
满足: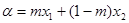 ,
,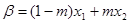 ,并且使得不等式
,并且使得不等式
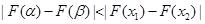 恒成立,求实数
恒成立,求实数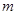 的取值范围.
的取值范围.
查看习题详情和答案>>
(本小题满分13分)省环保研究所对市中心每天环境放射性污染情况进行调查研究后,发现一天中环境综合放射性污染指数 与时刻
与时刻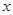 (时)的关系为
(时)的关系为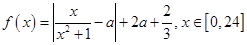 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且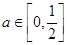 ,若用每天
,若用每天 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作 .
.
(1)令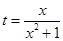 ,
,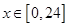 ,求t的取值范围;
,求t的取值范围;
(2)省政府规定,每天的综合放射性污染指数不得超过2,试问目前市中心的综合放射性污染指数是否超标?
查看习题详情和答案>>
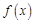 与时刻
与时刻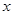 (时)的关系为
(时)的关系为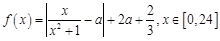 ,其中
,其中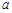 是与气象有关的参数,且
是与气象有关的参数,且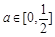 ,若用每天
,若用每天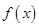 的最大值为当天的综合放射性污染指数,并记作
的最大值为当天的综合放射性污染指数,并记作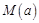 .
.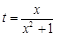 ,
,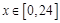 ,求t的取值范围;
,求t的取值范围;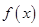 与时间x(小时)的关系为
与时间x(小时)的关系为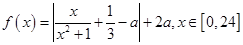 ,其中
,其中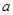 是与气象有关的参数,且
是与气象有关的参数,且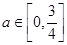 ,若用每天
,若用每天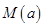 .
.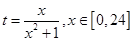 ,求t的取值范围;
,求t的取值范围;