网址:http://m.1010jiajiao.com/timu_id_540011[举报]
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
A
D
C
D
B
C
A
二、填空题(每小题4分,共24分)
11 数学理科.files/image245.gif) 12 10 13 144
12 10 13 144数学理科.files/image247.gif) 14
14 数学理科.files/image249.gif) 15
15 数学理科.files/image251.gif)
16 540
三、 解答题(共76分,以下各题文累积得分,其他解法请相应给分)
17解:(I)由题意得数学理科.files/image253.gif) ,即
,即数学理科.files/image255.gif) ,
,数学理科.files/image257.gif) ,……3分
,……3分
又数学理科.files/image259.gif) ,
,数学理科.files/image261.gif) ,……4分
,……4分
数学理科.files/image263.gif) ……6分
……6分
(II)数学理科.files/image265.gif) ,
,
数学理科.files/image267.gif) 于是
于是数学理科.files/image269.gif)
又数学理科.files/image271.gif) ……8分
……8分
又数学理科.files/image273.gif) ……10分
……10分
数学理科.files/image275.gif) ……12分
……12分
18 解:(I) 最大编号数学理科.files/image277.gif) 分别为3,4,5,6。
分别为3,4,5,6。数学理科.files/image279.gif) ,……2分
,……2分
数学理科.files/image281.gif) ……4分
……4分
数学理科.files/image283.gif) ,……6分
,……6分 数学理科.files/image285.gif) ……8分,即分布列为
……8分,即分布列为
数学理科.files/image277.gif)
3
4
5
6
数学理科.files/image153.gif)
数学理科.files/image289.gif)
数学理科.files/image291.gif)
数学理科.files/image293.gif)
数学理科.files/image063.gif)
(II)数学理科.files/image277.gif) 的数字期望
的数字期望数学理科.files/image297.gif) ……10分
……10分
数学理科.files/image299.gif)
数学理科.files/image277.gif) 的方差
的方差
……12分
19 解:(I)证明:连结数学理科.files/image302.gif) 是长方体,
是长方体,
数学理科.files/image304.gif) 面
面数学理科.files/image149.gif)
数学理科.files/image307.jpg) 又
又数学理科.files/image309.gif) 面
面数学理科.files/image149.gif) ,
,数学理科.files/image312.gif) ,又
,又数学理科.files/image149.gif) 是正方形,
是正方形,
数学理科.files/image315.gif)
数学理科.files/image317.gif) 面
面数学理科.files/image319.gif) ,即
,即数学理科.files/image321.gif) ……3分
……3分
又数学理科.files/image323.gif) ,
,数学理科.files/image325.gif) ……6分
……6分
(II)如图,以数学理科.files/image327.gif) 为原点建系,由题意的
为原点建系,由题意的数学理科.files/image329.gif)
数学理科.files/image331.gif) ……6分
……6分
于是数学理科.files/image333.gif)
数学理科.files/image335.gif) ,设
,设数学理科.files/image337.gif) 面
面数学理科.files/image339.gif)
不妨设数学理科.files/image341.gif) 由
由数学理科.files/image343.gif)
数学理科.files/image345.gif)
……8分
设数学理科.files/image347.gif) 面
面数学理科.files/image349.gif) ,不妨设
,不妨设数学理科.files/image351.gif)
数学理科.files/image353.gif) ……9分
……9分
若数学理科.files/image355.gif) 与
与数学理科.files/image357.gif) 的夹角
的夹角数学理科.files/image359.gif) ,则
,则数学理科.files/image361.gif) ……11分
……11分
据分析二面角数学理科.files/image161.gif) 是锐角,
是锐角,数学理科.files/image364.gif) 二面角
二面角数学理科.files/image161.gif) 的余弦值是
的余弦值是数学理科.files/image367.gif) ……12分
……12分
20 解:(I)由题意知数学理科.files/image369.gif) 故
故数学理科.files/image371.gif) ……1分
……1分
又数学理科.files/image373.gif) 设椭圆中心
设椭圆中心数学理科.files/image123.gif) 关于直线
关于直线数学理科.files/image169.gif) 的对称点为
的对称点为数学理科.files/image377.gif) ,
,
于是数学理科.files/image379.gif) 方程为
方程为数学理科.files/image381.gif) ……2分
……2分
由数学理科.files/image383.gif) 得线段
得线段数学理科.files/image379.gif) 的中点为(2,-1),从而
的中点为(2,-1),从而数学理科.files/image377.gif) 的横坐标为4
的横坐标为4
故数学理科.files/image385.gif) 椭圆的方程为
椭圆的方程为数学理科.files/image387.gif) =1……4分
=1……4分
(II)由题意知直线数学理科.files/image177.gif) 存在斜率,设直线
存在斜率,设直线数学理科.files/image177.gif) 的方程为
的方程为数学理科.files/image391.gif) 并整理得
并整理得数学理科.files/image393.gif) ①……6分
①……6分
由数学理科.files/image395.gif) ,得
,得数学理科.files/image397.gif) 又
又数学理科.files/image399.gif) 不合题意
不合题意
数学理科.files/image401.gif) ……8分
……8分
设点数学理科.files/image403.gif) ,则
,则数学理科.files/image405.gif)
由①知数学理科.files/image407.gif) ……9分
……9分
直线数学理科.files/image183.gif) 方程为
方程为数学理科.files/image410.gif) ……10分
……10分
令数学理科.files/image412.gif) 得
得数学理科.files/image414.gif) ,将
,将数学理科.files/image416.gif) 代入
代入
整理得 数学理科.files/image418.gif) ,再将
,再将数学理科.files/image420.gif) ,
,数学理科.files/image422.gif) 代入计算得
代入计算得数学理科.files/image424.gif)
数学理科.files/image364.gif) 直线
直线 数学理科.files/image427.gif) 轴相交于顶点(1,0),……12分
轴相交于顶点(1,0),……12分
21解:(I)数学理科.files/image429.gif) ……2分
……2分
数学理科.files/image431.gif)
① 数学理科.files/image433.gif) 若
若数学理科.files/image435.gif) ,则当
,则当数学理科.files/image437.gif) 或
或数学理科.files/image439.gif) 时
时数学理科.files/image441.gif) 时,
时,
内是增函数,在 数学理科.files/image443.gif) 内是减函数 ,……4分
内是减函数 ,……4分
② 若数学理科.files/image445.gif)
数学理科.files/image447.gif) 内是增函数,在
内是增函数,在数学理科.files/image449.gif) 内是减函数……6分
内是减函数……6分
(II)由题意知数学理科.files/image451.gif) 得
得数学理科.files/image453.gif) ……7分
……7分
数学理科.files/image455.gif) 恰有一根(含重根 )
恰有一根(含重根 )
数学理科.files/image457.gif) ……8分
……8分
又数学理科.files/image459.gif)
数学理科.files/image461.gif) 的值域为
的值域为数学理科.files/image463.gif) 和
和数学理科.files/image465.gif) 内是增函数,
内是增函数,数学理科.files/image195.gif) 在
在数学理科.files/image468.gif) 内是增函数,
内是增函数,
由题意的数学理科.files/image470.gif) 解得
解得数学理科.files/image472.gif) ……12分
……12分
当数学理科.files/image474.gif) 内是增函数,
内是增函数,数学理科.files/image195.gif) 在
在数学理科.files/image477.gif) 内是增函数
内是增函数
由题意得数学理科.files/image479.gif) 解得
解得数学理科.files/image481.gif)
综上知实数数学理科.files/image097.gif) 的取值范围为
的取值范围为数学理科.files/image484.gif) ……14分
……14分
22 解(I)设数学理科.files/image219.gif) 公差为
公差为数学理科.files/image487.gif) ,由
,由数学理科.files/image489.gif) 得
得数学理科.files/image491.gif) ……1分
……1分
数学理科.files/image364.gif) 数列
数列数学理科.files/image217.gif) 为3,5,7,9,7,5,3,……2分
为3,5,7,9,7,5,3,……2分
(II)数学理科.files/image495.gif) ……3分
……3分
又数学理科.files/image497.gif) =
=数学理科.files/image499.gif) ……4分
……4分
数学理科.files/image501.gif)
(III)所有可能的“对称数列”是①1,2,22数学理科.files/image503.gif)
②数学理科.files/image505.gif)
③数学理科.files/image507.gif)
④数学理科.files/image509.gif) ……9分
……9分
当
数学理科.files/image511.gif)
对于②当数学理科.files/image513.gif)
当
数学理科.files/image515.gif)
对于③当数学理科.files/image517.gif) 时,
时,数学理科.files/image519.gif)
当数学理科.files/image521.gif)
数学理科.files/image523.gif) 分
分
对于④当数学理科.files/image517.gif) 时,
时,数学理科.files/image519.gif)
当
数学理科.files/image527.gif)
若有穷数列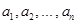 (
(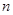 是正整数),满足
是正整数),满足 ,
, ,
, ,
,
 ,即
,即 (
( 是正整数,且
是正整数,且 ),就称该数列为“对称数列”.
),就称该数列为“对称数列”.
(1)已知数列 是项数为7的对称数列,且
是项数为7的对称数列,且 成等差数列,
成等差数列,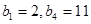 ,试写出
,试写出 的每一项.
的每一项.
(2)已知 是项数为
是项数为 的对称数列,且
的对称数列,且 构成首项为50,公差为
构成首项为50,公差为 的等差数列,数列
的等差数列,数列 的前
的前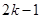 项和为
项和为 ,则当
,则当 为何值时,
为何值时, 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数 ,试写出所有项数不超过
,试写出所有项数不超过 的对称数列,使得
的对称数列,使得 成为数列中的连续项;当
成为数列中的连续项;当 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和 .
.
查看习题详情和答案>>
若有穷数列![]() (
(![]() 是正整数),满足
是正整数),满足![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() (
(![]() 是正整数,且
是正整数,且![]() ),就称该数列为“对称数列”.
),就称该数列为“对称数列”.
(1)已知数列![]() 是项数为7的对称数列,且
是项数为7的对称数列,且![]() 成等差数列,
成等差数列,![]() ,试写出
,试写出![]() 的每一项.
的每一项.
(2)已知![]() 是项数为
是项数为![]() 的对称数列,且
的对称数列,且![]() 构成首项为50,公差为
构成首项为50,公差为![]() 的等差数列,数列
的等差数列,数列![]() 的前
的前![]() 项和为
项和为![]() ,则当
,则当![]() 为何值时,
为何值时,![]() 取到最大值?最大值为多少?
取到最大值?最大值为多少?
(3)对于给定的正整数![]() ,试写出所有项数不超过
,试写出所有项数不超过![]() 的对称数列,使得
的对称数列,使得![]() 成为数列中的连续项;当
成为数列中的连续项;当![]() 时,试求其中一个数列的前2008项和
时,试求其中一个数列的前2008项和![]() .
.
(1)已知数列{bn}是项数为7的对称数列,且b1,b2,b3,b4成等差数列,b1=2,b4=11,试写出{bn}的每一项;
(2)已知{cn}是项数为2k-1(k≥1)的对称数列,且ck,ck+1,…,c2k-1构成首项为50,公差为-4的等差数列,数列{cn}的前2k-1项和为S2k-1,则当k为何值时,S2k-1取到最大值?最大值为多少?
(3)对于给定的正整数m>1,试写出所有项数不超过2m的对称数列,使得1,2,22,…,2m-1成为数列中的连续项;当m>1500时,试求其中一个数列的前2008项和S2008。
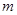 的有穷数列数集
的有穷数列数集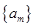 ,记
,记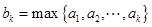
 ,即
,即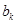 为
为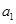 、
、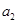 、
、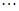 、
、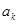 中的最大值,并称数列
中的最大值,并称数列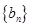 是
是 的控制数列.如
的控制数列.如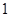 、
、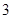 、
、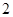 、
、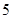 、
、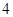 、
、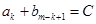 (
(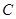 为常数,
为常数,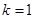 、
、