网址:http://m.1010jiajiao.com/timu_id_540006[举报]
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
A
D
C
D
B
C
A
二、填空题(每小题4分,共24分)
11 数学理科.files/image245.gif) 12 10 13 144
12 10 13 144数学理科.files/image247.gif) 14
14 数学理科.files/image249.gif) 15
15 数学理科.files/image251.gif)
16 540
三、 解答题(共76分,以下各题文累积得分,其他解法请相应给分)
17解:(I)由题意得数学理科.files/image253.gif) ,即
,即数学理科.files/image255.gif) ,
,数学理科.files/image257.gif) ,……3分
,……3分
又数学理科.files/image259.gif) ,
,数学理科.files/image261.gif) ,……4分
,……4分
数学理科.files/image263.gif) ……6分
……6分
(II)数学理科.files/image265.gif) ,
,
数学理科.files/image267.gif) 于是
于是数学理科.files/image269.gif)
又数学理科.files/image271.gif) ……8分
……8分
又数学理科.files/image273.gif) ……10分
……10分
数学理科.files/image275.gif) ……12分
……12分
18 解:(I) 最大编号数学理科.files/image277.gif) 分别为3,4,5,6。
分别为3,4,5,6。数学理科.files/image279.gif) ,……2分
,……2分
数学理科.files/image281.gif) ……4分
……4分
数学理科.files/image283.gif) ,……6分
,……6分 数学理科.files/image285.gif) ……8分,即分布列为
……8分,即分布列为
数学理科.files/image277.gif)
3
4
5
6
数学理科.files/image153.gif)
数学理科.files/image289.gif)
数学理科.files/image291.gif)
数学理科.files/image293.gif)
数学理科.files/image063.gif)
(II)数学理科.files/image277.gif) 的数字期望
的数字期望数学理科.files/image297.gif) ……10分
……10分
数学理科.files/image299.gif)
数学理科.files/image277.gif) 的方差
的方差
……12分
19 解:(I)证明:连结数学理科.files/image302.gif) 是长方体,
是长方体,
数学理科.files/image304.gif) 面
面数学理科.files/image149.gif)
数学理科.files/image307.jpg) 又
又数学理科.files/image309.gif) 面
面数学理科.files/image149.gif) ,
,数学理科.files/image312.gif) ,又
,又数学理科.files/image149.gif) 是正方形,
是正方形,
数学理科.files/image315.gif)
数学理科.files/image317.gif) 面
面数学理科.files/image319.gif) ,即
,即数学理科.files/image321.gif) ……3分
……3分
又数学理科.files/image323.gif) ,
,数学理科.files/image325.gif) ……6分
……6分
(II)如图,以数学理科.files/image327.gif) 为原点建系,由题意的
为原点建系,由题意的数学理科.files/image329.gif)
数学理科.files/image331.gif) ……6分
……6分
于是数学理科.files/image333.gif)
数学理科.files/image335.gif) ,设
,设数学理科.files/image337.gif) 面
面数学理科.files/image339.gif)
不妨设数学理科.files/image341.gif) 由
由数学理科.files/image343.gif)
数学理科.files/image345.gif)
……8分
设数学理科.files/image347.gif) 面
面数学理科.files/image349.gif) ,不妨设
,不妨设数学理科.files/image351.gif)
数学理科.files/image353.gif) ……9分
……9分
若数学理科.files/image355.gif) 与
与数学理科.files/image357.gif) 的夹角
的夹角数学理科.files/image359.gif) ,则
,则数学理科.files/image361.gif) ……11分
……11分
据分析二面角数学理科.files/image161.gif) 是锐角,
是锐角,数学理科.files/image364.gif) 二面角
二面角数学理科.files/image161.gif) 的余弦值是
的余弦值是数学理科.files/image367.gif) ……12分
……12分
20 解:(I)由题意知数学理科.files/image369.gif) 故
故数学理科.files/image371.gif) ……1分
……1分
又数学理科.files/image373.gif) 设椭圆中心
设椭圆中心数学理科.files/image123.gif) 关于直线
关于直线数学理科.files/image169.gif) 的对称点为
的对称点为数学理科.files/image377.gif) ,
,
于是数学理科.files/image379.gif) 方程为
方程为数学理科.files/image381.gif) ……2分
……2分
由数学理科.files/image383.gif) 得线段
得线段数学理科.files/image379.gif) 的中点为(2,-1),从而
的中点为(2,-1),从而数学理科.files/image377.gif) 的横坐标为4
的横坐标为4
故数学理科.files/image385.gif) 椭圆的方程为
椭圆的方程为数学理科.files/image387.gif) =1……4分
=1……4分
(II)由题意知直线数学理科.files/image177.gif) 存在斜率,设直线
存在斜率,设直线数学理科.files/image177.gif) 的方程为
的方程为数学理科.files/image391.gif) 并整理得
并整理得数学理科.files/image393.gif) ①……6分
①……6分
由数学理科.files/image395.gif) ,得
,得数学理科.files/image397.gif) 又
又数学理科.files/image399.gif) 不合题意
不合题意
数学理科.files/image401.gif) ……8分
……8分
设点数学理科.files/image403.gif) ,则
,则数学理科.files/image405.gif)
由①知数学理科.files/image407.gif) ……9分
……9分
直线数学理科.files/image183.gif) 方程为
方程为数学理科.files/image410.gif) ……10分
……10分
令数学理科.files/image412.gif) 得
得数学理科.files/image414.gif) ,将
,将数学理科.files/image416.gif) 代入
代入
整理得 数学理科.files/image418.gif) ,再将
,再将数学理科.files/image420.gif) ,
,数学理科.files/image422.gif) 代入计算得
代入计算得数学理科.files/image424.gif)
数学理科.files/image364.gif) 直线
直线 数学理科.files/image427.gif) 轴相交于顶点(1,0),……12分
轴相交于顶点(1,0),……12分
21解:(I)数学理科.files/image429.gif) ……2分
……2分
数学理科.files/image431.gif)
① 数学理科.files/image433.gif) 若
若数学理科.files/image435.gif) ,则当
,则当数学理科.files/image437.gif) 或
或数学理科.files/image439.gif) 时
时数学理科.files/image441.gif) 时,
时,
内是增函数,在 数学理科.files/image443.gif) 内是减函数 ,……4分
内是减函数 ,……4分
② 若数学理科.files/image445.gif)
数学理科.files/image447.gif) 内是增函数,在
内是增函数,在数学理科.files/image449.gif) 内是减函数……6分
内是减函数……6分
(II)由题意知数学理科.files/image451.gif) 得
得数学理科.files/image453.gif) ……7分
……7分
数学理科.files/image455.gif) 恰有一根(含重根 )
恰有一根(含重根 )
数学理科.files/image457.gif) ……8分
……8分
又数学理科.files/image459.gif)
数学理科.files/image461.gif) 的值域为
的值域为数学理科.files/image463.gif) 和
和数学理科.files/image465.gif) 内是增函数,
内是增函数,数学理科.files/image195.gif) 在
在数学理科.files/image468.gif) 内是增函数,
内是增函数,
由题意的数学理科.files/image470.gif) 解得
解得数学理科.files/image472.gif) ……12分
……12分
当数学理科.files/image474.gif) 内是增函数,
内是增函数,数学理科.files/image195.gif) 在
在数学理科.files/image477.gif) 内是增函数
内是增函数
由题意得数学理科.files/image479.gif) 解得
解得数学理科.files/image481.gif)
综上知实数数学理科.files/image097.gif) 的取值范围为
的取值范围为数学理科.files/image484.gif) ……14分
……14分
22 解(I)设数学理科.files/image219.gif) 公差为
公差为数学理科.files/image487.gif) ,由
,由数学理科.files/image489.gif) 得
得数学理科.files/image491.gif) ……1分
……1分
数学理科.files/image364.gif) 数列
数列数学理科.files/image217.gif) 为3,5,7,9,7,5,3,……2分
为3,5,7,9,7,5,3,……2分
(II)数学理科.files/image495.gif) ……3分
……3分
又数学理科.files/image497.gif) =
=数学理科.files/image499.gif) ……4分
……4分
数学理科.files/image501.gif)
(III)所有可能的“对称数列”是①1,2,22数学理科.files/image503.gif)
②数学理科.files/image505.gif)
③数学理科.files/image507.gif)
④数学理科.files/image509.gif) ……9分
……9分
当
数学理科.files/image511.gif)
对于②当数学理科.files/image513.gif)
当
数学理科.files/image515.gif)
对于③当数学理科.files/image517.gif) 时,
时,数学理科.files/image519.gif)
当数学理科.files/image521.gif)
数学理科.files/image523.gif) 分
分
对于④当数学理科.files/image517.gif) 时,
时,数学理科.files/image519.gif)
当
数学理科.files/image527.gif)
已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线![]() 相切.
相切.
(I)求椭圆![]() 的方程;
的方程;
(II)设![]() ,
,![]()
![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() ,证明直线
,证明直线![]() 与
与![]() 轴相交于定点
轴相交于定点![]() ;
;
(Ⅲ)在(II)的条件下,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]()
![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
(本题满分12分)已知椭圆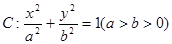 的离心率为
的离心率为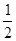 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线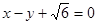 相切.
相切.
(I)求椭圆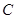 的方程;
的方程;
(II)设P(4,0),A,B是椭圆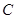 上关于
上关于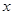 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接 交椭圆
交椭圆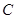 于另一点
于另一点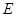 ,证明直线
,证明直线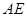 与
与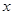 轴相交于定点
轴相交于定点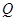 ;
;
(Ⅲ)在(II)的条件下,过点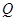 的直线与椭圆
的直线与椭圆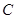 交于
交于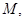
 两点,求
两点,求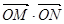 的取值范围.
的取值范围.
查看习题详情和答案>>
 ,它的一个顶点恰好是抛物线x2=4
,它的一个顶点恰好是抛物线x2=4 的焦点.
的焦点.(I)求椭圆C的标准方程;
(II)若A、B是椭圆C上关x轴对称的任意两点,设P(-4,0),连接PA交椭圆C于另一点E,求证:直线BE与x轴相交于定点M;
(III)设O为坐标原点,在(II)的条件下,过点M的直线交椭圆C于S、T两点,求
 •
• 的取值范围.
的取值范围.查看习题详情和答案>>
 ,它的一个顶点恰好是抛物线y=
,它的一个顶点恰好是抛物线y= x2的焦点.
x2的焦点. •
• 的取值范围.
的取值范围.