网址:http://m.1010jiajiao.com/timu_id_539957[举报]
一、选择题(每小题5分,共50分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
D
B
D
A
B
B
A
二、填空题(每小题4分,共24分)
11.数学文科.files/image226.gif) ; 12.
; 12.数学文科.files/image228.gif) ; 13.
; 13.数学文科.files/image230.gif) ; 14.
; 14.数学文科.files/image232.gif) 15.
15.数学文科.files/image234.gif) 16.1
16.1
三、解答题(本大题共6小题,共76分,以下各题为累计得分,其他解法请相应给分)
17.解(I)由题意得数学文科.files/image236.gif) 即
即数学文科.files/image238.gif)
又数学文科.files/image240.gif)
数学文科.files/image242.gif)
(Ⅱ)数学文科.files/image244.gif)
数学文科.files/image246.gif) 于是
于是数学文科.files/image248.gif)
又数学文科.files/image250.gif) 又
又数学文科.files/image252.gif)
又数学文科.files/image254.gif)
数学文科.files/image256.gif)
18.解:(I)任取3个球的基本情况有(1,2,3),(1,2,3数学文科.files/image258.gif) ),(1,2,4),(1,2,5),(1,3,3
),(1,2,4),(1,2,5),(1,3,3数学文科.files/image258.gif) )(1,3,4)
)(1,3,4)
(1,3,5),(1,3数学文科.files/image258.gif) ,4),(1,3
,4),(1,3数学文科.files/image258.gif) ,5),(1,4,5),(2,3,3
,5),(1,4,5),(2,3,3数学文科.files/image258.gif) ),(2,3,4),(2,3,5),(2,3
),(2,3,4),(2,3,5),(2,3数学文科.files/image258.gif) ,4),(2,3
,4),(2,3数学文科.files/image258.gif) ,5),(2
,5),(2
,4,5),(3,3数学文科.files/image258.gif) ,4),(3,3
,4),(3,3数学文科.files/image258.gif) ,5),(3,4,5),(3
,5),(3,4,5),(3数学文科.files/image258.gif) ,4,5)共20种,
,4,5)共20种,
其中最大编号为4的有(1,2,4),(1,3,4),(1,3数学文科.files/image258.gif) ,4),(2,3,4),(2,3
,4),(2,3,4),(2,3数学文科.files/image258.gif) ,4),
,4),
(3,3数学文科.files/image258.gif) ,4)共6种,所以3个球中最大编号为4的概率为
,4)共6种,所以3个球中最大编号为4的概率为数学文科.files/image260.gif)
(Ⅱ)3个球中有1个编号为3的有(1,2,3),(1,2,3数学文科.files/image258.gif) ),(1,3,4),(1,3,5),(1,
),(1,3,4),(1,3,5),(1,
3数学文科.files/image258.gif) ,4),(1,3
,4),(1,3数学文科.files/image258.gif) ,5),(2,3,4),(2,3,5),(2,3
,5),(2,3,4),(2,3,5),(2,3数学文科.files/image258.gif) ,4),(2,3
,4),(2,3数学文科.files/image258.gif) ,5),(3,4,5),(3
,5),(3,4,5),(3数学文科.files/image258.gif) ,
,
4,5)共12种
有2个编号为3的有(1,3,3数学文科.files/image258.gif) ),(2,3,3
),(2,3,3数学文科.files/image258.gif) ),(3,3
),(3,3数学文科.files/image258.gif) ,4),(3,3
,4),(3,3数学文科.files/image258.gif) ,5)共4种
,5)共4种
所以3个球中至少有个编号为3的概率是数学文科.files/image262.gif)
19.解:(I)数学文科.files/image264.gif) 是长方体,
是长方体,数学文科.files/image266.gif)
数学文科.files/image268.gif) 平面
平面数学文科.files/image184.gif) ,又
,又数学文科.files/image271.gif) 面
面数学文科.files/image184.gif) ,
,
数学文科.files/image274.gif) 又
又数学文科.files/image184.gif) 是正方形。
是正方形。数学文科.files/image277.gif) ,又
,又数学文科.files/image279.gif) ,
,数学文科.files/image281.gif) 面
面数学文科.files/image283.gif)
(Ⅱ)数学文科.files/image285.gif)
(Ⅲ)连结数学文科.files/image287.gif) 有
有数学文科.files/image289.gif)
又有上知数学文科.files/image291.gif) ,
,数学文科.files/image293.gif)
由题意得数学文科.files/image295.gif)
数学文科.files/image297.gif) 于是可得
于是可得数学文科.files/image299.gif) 上的高为6
上的高为6
数学文科.files/image301.gif)
20.解:(I)数学文科.files/image303.gif) ‘
‘
又数学文科.files/image305.gif) 令
令数学文科.files/image307.gif) ,得
,得数学文科.files/image309.gif)
①若数学文科.files/image311.gif) ,则当
,则当数学文科.files/image313.gif) 或
或数学文科.files/image315.gif) 时
时数学文科.files/image317.gif) 。当
。当数学文科.files/image319.gif) 时,
时,数学文科.files/image321.gif)
数学文科.files/image323.gif) 在
在数学文科.files/image325.gif) 和
和数学文科.files/image327.gif) 内是增函数,在
内是增函数,在数学文科.files/image329.gif) 内是减函数,
内是减函数,
②若数学文科.files/image331.gif) 则当
则当数学文科.files/image333.gif) 或
或数学文科.files/image335.gif) 时,
时,数学文科.files/image317.gif) 当
当数学文科.files/image338.gif) 时,
时,数学文科.files/image321.gif)
数学文科.files/image323.gif) 在
在数学文科.files/image342.gif) 和
和数学文科.files/image344.gif) 内是增函数,在
内是增函数,在数学文科.files/image346.gif) 内是减函数
内是减函数
(Ⅱ)当数学文科.files/image311.gif) 时,
时,数学文科.files/image106.gif) 在
在数学文科.files/image325.gif) 和
和数学文科.files/image327.gif) 内是增函数,
内是增函数,数学文科.files/image352.gif) 故
故
数学文科.files/image205.gif) 在
在数学文科.files/image355.gif) 内是增函数。
内是增函数。
由题意得数学文科.files/image357.gif) 解得
解得数学文科.files/image359.gif)
当数学文科.files/image361.gif) 时,
时,数学文科.files/image106.gif) 在
在数学文科.files/image342.gif) 和
和数学文科.files/image344.gif) 内是增函数,
内是增函数,数学文科.files/image205.gif) 在
在数学文科.files/image367.gif) 内是增函数。
内是增函数。
由题意得数学文科.files/image369.gif) 解得
解得数学文科.files/image371.gif)
综上知实数数学文科.files/image119.gif) 的取值范围为
的取值范围为数学文科.files/image374.gif)
(21)解:(1)设数学文科.files/image376.gif) 的公比为
的公比为数学文科.files/image378.gif) ,由题意有
,由题意有数学文科.files/image380.gif)
解得数学文科.files/image382.gif) 或
或数学文科.files/image384.gif) (舍)
(舍)
数学文科.files/image386.gif)
(Ⅱ)数学文科.files/image388.gif) ,
,数学文科.files/image390.gif) 是以2为首项,-1为公差的等差数列
是以2为首项,-1为公差的等差数列
数学文科.files/image392.gif)
(Ⅲ)显然数学文科.files/image394.gif)
又数学文科.files/image396.gif) 当
当数学文科.files/image398.gif) 时,
时,数学文科.files/image400.gif)
数学文科.files/image402.gif) 当
当数学文科.files/image398.gif) 时,
时,数学文科.files/image405.gif)
数学文科.files/image407.gif)
数学文科.files/image402.gif) 当
当数学文科.files/image410.gif) 时,
时,数学文科.files/image412.gif) 故当
故当数学文科.files/image414.gif) 或
或数学文科.files/image398.gif) 时
时数学文科.files/image405.gif)
22.解:(I)由题意知数学文科.files/image418.gif) 故
故数学文科.files/image420.gif)
又数学文科.files/image422.gif) 设椭圆中心
设椭圆中心数学文科.files/image151.gif) 关于直线
关于直线数学文科.files/image425.gif) 的对称点为
的对称点为数学文科.files/image427.gif) 。
。
于是数学文科.files/image429.gif) 方程为
方程为数学文科.files/image431.gif)
由数学文科.files/image433.gif) 得线段
得线段数学文科.files/image429.gif) 的中点为(2,-1),从而
的中点为(2,-1),从而数学文科.files/image427.gif) 的横坐标为4,
的横坐标为4,
故数学文科.files/image437.gif)
数学文科.files/image402.gif) 椭圆的方程为
椭圆的方程为数学文科.files/image440.gif)
(Ⅱ)由题意知直线数学文科.files/image442.gif) 存在斜率,设直线
存在斜率,设直线数学文科.files/image442.gif) 的方程为
的方程为数学文科.files/image445.gif) 代入
代入数学文科.files/image440.gif) 并
并
整理得数学文科.files/image448.gif)
由数学文科.files/image450.gif) 得
得数学文科.files/image452.gif) 又
又数学文科.files/image454.gif) 不合题意。
不合题意。
数学文科.files/image456.gif) 或
或数学文科.files/image458.gif)
设点数学文科.files/image460.gif) 则
则数学文科.files/image462.gif)
由①知数学文科.files/image464.gif)
直线数学文科.files/image466.gif) 方程为
方程为数学文科.files/image468.gif)
令数学文科.files/image470.gif) 得
得数学文科.files/image472.gif) 将
将数学文科.files/image474.gif) 代入
代入
整理得数学文科.files/image476.gif)
再将数学文科.files/image464.gif) 代入计算得
代入计算得数学文科.files/image479.gif)
数学文科.files/image402.gif) 直线
直线数学文科.files/image466.gif) 与
与数学文科.files/image084.gif) 轴相交于定点(1,0)
轴相交于定点(1,0)

 ) C.[-8,1] D.[-9,1]
) C.[-8,1] D.[-9,1]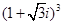 =( )
=( ) D.
D.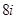
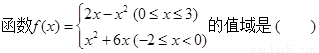
 ) C. [-8,1] D. [-9,1]
) C. [-8,1] D. [-9,1]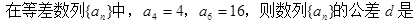 ( )
( )
 )
)