网址：http://m.1010jiajiao.com/timu_id_539004[举报]
一、选择题
1 B
二、填空题
11 192 12
286 13 
14
15
840 16 
三、解答题
17 （本题12分）
解：（I）
2分
（II）
8分
由已知条件
根据正弦定理，得
10分
12分
18 （本题12分）
解：（I）在7人中选出3人，总的结果数是
种， （2分）
记“被选中的3人中至多有1名女生”为事件A，则A包含两种情形：
①被选中的是1名女生，2名男生的结果数是
，
②被选中的是3名男生的结果数是
4分
至多选中1名女生的概率为
6分
（II）由题意知随机变量
可能的取值为：0，1，2，3，则有
，
8分
∴
0
1
2
3
P
10分
∴的数学期望
12分
19 （本题12分）
解：（I）连接PO，以OA，OB，OP所在的直线为x轴，y轴，z轴
建立如图所示的空间直角坐标系。 2分
∵正四棱锥的底面边长和侧棱长都是2。
∴
∴
（II）∵
∴
是平面PDB的一个法向量。 8分
由（I）得
设平面BMP的一个法向量为
则由
，得
，不妨设c=1
得平面BMP的一个法向量为
10分
∵二面角M―PB―D小于90°
∴二面角M―PB―D的余弦值为
12分
20 （本题12分）
解：（I）由已知得
2分
由
，得 4分
即
。解得k=50或
（舍去）
6分
（II）由
，得
8分
9分
是等差数列
则
11分
12分
21 （本题14分）
解：（I）依题意得
2分
把
解得
∴椭圆的方程为
4分
（II）由（I）得
，设
，如图所示，
∵M点在椭圆上，
∴
①
∵M点异于顶点A、B，
∴
由P、A、M三点共线，可得
，
从而
7分
∴
② 8分
将①式代入②式化简得
10分
∵
∴
12分
于是∠MBP为锐角，从而∠MBN为钝角，
∴点B在以MN为直径的圆内。 14分
22 （本题14分）
解：（I）
，
令
2分
而
∴当
4分
（II）设函数g(x)在[0，2]上的值域是A，
∵若对任意
∴
6分
①当
，
∴函数
上单调递减。
∵
∴
； 8分
②当
令
（舍去） 9分
（i）当
时，
的变化如下表：
（ii）当
∴函数g(x)在（0，2）上单调递减。
综上可知，实数a的取值范围是
（1）求函数y=T（x2）和y=（T（x））2的解析式；
（2）是否存在实数a，使得T（x）+a2=T（x+a）恒成立，若存在，求出a的值，若不存在，请说明理由；
（3）定义Tn+1（x）=Tn（T（x）），且T1（x）=T（x），（n∈N*）
①当
时，求y=T4（x）的解析式；已知下面正确的命题：当
时（i∈N*，1≤i≤15），都有
恒成立．②若方程T4（x）=kx恰有15个不同的实数根，确定k的取值；并求这15个不同的实数根的和．
查看习题详情和答案>>
|
（1）求函数y=T（x2）和y=（T（x））2的解析式；
（2）是否存在实数a，使得T（x）+a2=T（x+a）恒成立，若存在，求出a的值，若不存在，请说明理由；
（3）定义Tn+1（x）=Tn（T（x）），且T1（x）=T（x），（n∈N*）
①当x∈[ 0 ，
| 1 |
| 16 |
已知下面正确的命题：当x∈[
| i-1 |
| 16 |
| i+1 |
| 16 |
| i |
| 8 |
②若方程T4（x）=kx恰有15个不同的实数根，确定k的取值；并求这15个不同的实数根的和．
（1）判断数列{an}：an=1-2n和数列{bn}：bn=1-2n是否为集合A或B中的元素？
（2）已知数列an=(n-k)3，研究{an}是否为集合A或B中的元素；若是，求出实数k的取值范围；若不是，请说明理由．
（3）已an=31(-1)i•log2n(i∈Z，n∈N*)，若{an}为集合B中的元素，求满足不等式|2n-an|＜60的n的值组成的集合．
，其中a∈R．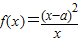
，其中a∈R．