网址:http://m.1010jiajiao.com/timu_id_538861[举报]
三、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
D
A
B
B
D
B
D
A
B
C
B
四、填空题
13.2 14. 31 15. .files/image185.gif) 16. 2.
16. 2.
三、解答题
17.解:(Ⅰ).files/image187.gif)
.files/image189.gif)
.files/image191.gif) .
.
.files/image193.gif) 的最小正周期
的最小正周期.files/image195.gif) .
.
(Ⅱ)由.files/image197.gif) 解得
解得
.files/image199.gif)
∴ .files/image097.gif) 的单调递增区间为
的单调递增区间为.files/image201.gif) 。
。
18.(I)解:记这两套试验方案在一次试验中均不成功的事件为A,则至少有一套试验成功的事件为.files/image203.gif) 由题意,这两套试验方案在一次试验中不成功的概率均为1-p.
由题意,这两套试验方案在一次试验中不成功的概率均为1-p.
所以,.files/image205.gif) , 从而,
, 从而,.files/image207.gif)
令.files/image209.gif)
(II)解:ξ的可取值为0,1,2.
.files/image211.gif)
.files/image213.gif)
所以ξ的分布列为
ξ
0
1
2
P
0.49
0.42
0.09
ξ的数学期望.files/image215.gif)
19.(Ⅰ)取DC的中点E.
∵ABCD是边长为.files/image045.gif) 的菱形,
的菱形,.files/image145.gif) ,∴BE⊥CD.
,∴BE⊥CD.
∵.files/image147.gif) 平面
平面.files/image149.gif) , BE
, BE.files/image037.gif) 平面
平面.files/image149.gif) ,∴
,∴.files/image147.gif) BE.
BE.
∴BE⊥平面PDC.∠BPE为求直线PB与平面PDC所成的角.
∵BE=.files/image218.gif) ,PE=
,PE=.files/image220.gif) ,∴
,∴.files/image222.gif) =
=.files/image224.gif) =
=.files/image226.gif) .
.
(Ⅱ)连接AC、BD交于点O,因为ABCD是菱形,所以AO⊥BD.
∵.files/image147.gif) 平面
平面.files/image149.gif) , AO
, AO.files/image037.gif) 平面
平面.files/image149.gif) ,
,
∴.files/image228.gif) PD. ∴AO⊥平面PDB.
PD. ∴AO⊥平面PDB.
作OF⊥PB于F,连接AF,则AF⊥PB.
故∠AFO就是二面角A-PB-D的平面角.
∵AO=.files/image218.gif) ,OF=
,OF=.files/image231.gif) ,∴
,∴.files/image233.gif) =
=.files/image235.gif) .
.
20.解: (Ⅰ).files/image237.gif) 在
在.files/image239.gif) 恒成立,
恒成立,
所以.files/image241.gif) ,
,.files/image243.gif) .
.
又.files/image245.gif) 在
在.files/image247.gif) 恒成立,
恒成立,
所以 .files/image249.gif) ,
,.files/image251.gif) .
.
从而有.files/image253.gif) .
.
故.files/image255.gif) ,
,.files/image257.gif) .
.
(Ⅱ)令.files/image259.gif) ,
,
则.files/image261.gif)
.files/image263.gif)
所以.files/image265.gif) 在
在.files/image267.gif) 上是减函数,在
上是减函数,在.files/image269.gif) 上是增函数,
上是增函数,
从而当.files/image271.gif) 时,
时,.files/image273.gif) .
.
所以方程.files/image275.gif) 在
在.files/image277.gif) 只有一个解
只有一个解.files/image279.gif) .
.
21.证明:由.files/image281.gif) 是关于x的方程
是关于x的方程.files/image283.gif) 的两根得
的两根得
.files/image285.gif) 。
。
.files/image287.gif)
.files/image289.gif) ,
,.files/image291.gif)
.files/image293.gif) 是等差数列。
是等差数列。
(2)由(1)知.files/image295.gif)
.files/image297.gif)
.files/image299.gif) 。
。
.files/image301.gif) 。
。
又.files/image303.gif) 符合上式,
符合上式,.files/image305.gif) 。
。
(3).files/image307.gif) ①
①
.files/image309.gif) ②
②
①―②得 .files/image311.gif) 。
。
.files/image313.gif)
.files/image315.gif)
.files/image317.gif) 。
。
22.解:(1)由题意.files/image319.gif)
.files/image321.gif)
(2)由(1)知:.files/image323.gif) (x>0)
(x>0)
.files/image325.gif)
令h(x)=px2-2x+p.要使g(x)在(0,+∞)为增函数,只需h(x)在(0,+∞)满足:h(x)≥0恒成立。即px2-2x+p≥0。
.files/image327.gif) 上恒成立
上恒成立
又.files/image329.gif)
所以.files/image331.gif)
(3)证明:①即证 lnx-x+1≤0 (x>0),
设.files/image333.gif) .
.
当x∈(0,1)时,k′(x)>0,∴k(x)为单调递增函数;
当x∈(1,∞)时,k′(x)<0,∴k(x)为单调递减函数;
∴x=1为k(x)的极大值点,
∴k(x)≤k(1)=0.
即lnx-x+1≤0,∴lnx≤x-1.
②由①知lnx≤x-1,又x>0,.files/image335.gif)
.files/image337.gif)
.files/image339.gif)
(1)研究此函数的定义域的所有可能情况(每一种可能情况用一个集合表示);
(2)将函数定义域中各元素之和记为S,试求S=3k+1(k∈Z)的概率.
(1)研究此函数的定义域的所有可能情况(每一种可能情况用一个集合表示);
(2)将函数定义域中各元素之和记为S,试求S=3k+1(k∈Z)的概率.
查看习题详情和答案>>
已知函数
(Ⅰ)若函数f(x)在[1,2]上是减函数,求实数a的取值范围;
(Ⅱ)令g(x)= f(x)-x2,是否存在实数a,当x∈(0,e](e是自然常数)时,函数g(x)的最小值是3,若存在,求出a的值;若不存在,说明理由;
(Ⅲ)当x∈(0,e]时,证明:
【解析】本试题主要是考查了导数在研究函数中的运用。第一问中利用函数f(x)在[1,2]上是减函数,的导函数恒小于等于零,然后分离参数求解得到a的取值范围。第二问中,
假设存在实数a,使 有最小值3,利用
有最小值3,利用 ,对a分类讨论,进行求解得到a的值。
,对a分类讨论,进行求解得到a的值。
第三问中,
因为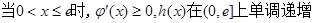 ,这样利用单调性证明得到不等式成立。
,这样利用单调性证明得到不等式成立。
解:(Ⅰ) 
(Ⅱ) 
(Ⅲ)见解析
查看习题详情和答案>>
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求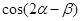 .
.
【解析】本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角关系是
,得到三角关系是 ,结合
,结合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,结合二倍角公式
,结合二倍角公式 ,和
,和 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴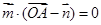 ,即
,即 ① …………2分
① …………2分
又 ② 由①②联立方程解得,
② 由①②联立方程解得,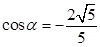 ,
,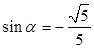 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即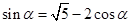 ,①……2分
,①……2分
又 ②
②
将①代入②中,可得 ③ …………………4分
③ …………………4分
将③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,从而
,从而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
综上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
综上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
查看习题详情和答案>>
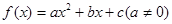 满足
满足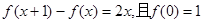 。
。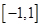 上,
上,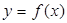 的图象恒在
的图象恒在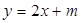 的图象上方,试确定实数
的图象上方,试确定实数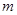 的取值范围。
的取值范围。