摘要：(3)设AFBD=O.则AO⊥BD.∵PB⊥平面ABCD.∴平面PBD⊥平面ABCD∴AO⊥平面PBD.过O作OH⊥PD于H.连AH.由三垂线定理知∠AHO为二面角A―PD―B的平面角.由(2)及O为BD的中点.知H为DE的中点.
网址：http://m.1010jiajiao.com/timu_id_537306[举报]
已知圆O的方程为x2+y2=1和点A（a，0），设圆O与x轴交于P、Q两点，M是圆OO上异于P、Q的任意一点，过点A（a，0）且与x轴垂直的直线为l，直线PM交直线l于点E，直线QM交直线l于点F．
（1）若a=3，直线l1过点A（3，0），且与圆O相切，求直线l1的方程；
（2）证明：若a=3，则以EF为直径的圆C总过定点，并求出定点坐标；
（3）若以EF为直径的圆C过定点，探求a的取值范围．
查看习题详情和答案>>
（1）若a=3，直线l1过点A（3，0），且与圆O相切，求直线l1的方程；
（2）证明：若a=3，则以EF为直径的圆C总过定点，并求出定点坐标；
（3）若以EF为直径的圆C过定点，探求a的取值范围．
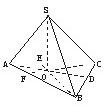已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c，设O为S在底面ABC上的射影．求证：（1）O为△ABC的垂心；
（2）O在△ABC内；
（3）设SO=h，则
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| h2 |
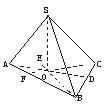已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c，设O为S在底面ABC上的射影．
+
+
=
．
+
+
=
．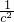