B M R A N ——青夏教育精英家教网——

摘要：B M R A N Q D K S P C 证:连结AC.在△ABC中.∵AM=MB.CN=NB.∴MN∥AC在△ADC中.∵AQ=QD.CP=PD.∴QP∥AC∴MN∥QP同理.连结BD可证MQ∥NP∴MNPQ是平行四边形取AC的中点K.连BK.DK∵AB=BC.∴BK⊥AC.∵AD=DC.∴DK⊥AC因此平面BKD与AC垂直∵BD在平面BKD内.∴BD⊥AC∵MQ∥BD.QP∥AC.∴MQ⊥QP.即∠MQP为直角故MNPQ是矩形八． Y x2=2qy y2=2px A1 O A2 A3 X 抛物线y2=2px的内接三角形有两边与抛物线x2=2qy相切.证明这个三角形的第三边也与x2=2qy相切

网址：http://m.1010jiajiao.com/timu_id_5365[举报]

下列各命题中，不正确的命题的个数为（）

①=|a| ②m(λa)·b=(mλ)a·b(m,λ∈R)③a·(b+c)=(b+c)·a ④a²b=b²a

A.4 B.3 C.2 D.1

查看习题详情和答案>>

（2012•包头一模）有下列命题：
①设集合M={x|0＜x≤3}，N={x|0＜x≤2}，则“a∈M”是“a∈N”的充分而不必要条件；
②命题“若a∈M，则b∉M”的逆否命题是：若b∈M，则a∉M；
③若p∧q是假命题，则p，q都是假命题；
④命题P：“?x0∈R，

-x0-1＞0”的否定￢P：“?x∈R，x²-x-1≤0”
则上述命题中为真命题的是（　　）

A．①②③④

查看习题详情和答案>>

设a,b,c,d,n,m∈R⁺,且P=,Q=,则P,Q之间的大小关系是…( )

A.P≥Q B.P≤Q

C.P=Q D.P,Q大小关系不确定

查看习题详情和答案>>

已知a,b,m,n∈R⁺,且m+n=1,设T=,Q=,则( )

A.T＞Q B.T≥Q

C.T＜Q D.T≤Q

查看习题详情和答案>>

定义平面向量之间的一种运算“⊙”如下：对任意的向量a=（m，n），b=（p，q），令a⊙b=（m+p，n-q），已知a=（cosθ，3），b=

（θ∈R），点N（x，y）满足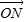

=a⊙b（其中O为坐标原点），则

的最大值为（）
A．

D．2
查看习题详情和答案>>