摘要:解:(Ⅰ) 2分 4分 由得: ∴对称中心的横坐标为. 6分 (Ⅱ)由已知得≥ 8分 又x是△ABC的内角.∴x的取值范围是 10分 这时..∴≤1 故函数f (x)的值域是---12分 18.解:(Ⅰ)体育教师不坐后排记为事件A.则.-----4分(Ⅱ)每位考生测试合格的概率.测试不合格的概率为则.即.∴.---------------8分(Ⅲ)∵- ∴ ----12分
网址:http://m.1010jiajiao.com/timu_id_5351[举报]
某市高三数学抽样考试中,对90分以上(含90分) 的成绩进行统计,其频率分布图如图所示,已知130~140分数段的人数为90,90~100分数段的人数为a,则下图所示程序框图的运算结果为(注:n!=1×2×3×…×n,如5!=1×2×3×4×5)( )


A.800! B.810! C.811! D.812!
查看习题详情和答案>>
设椭圆 (常数
(常数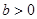 )的左右焦点分别为
)的左右焦点分别为 ,
, 是直线
是直线 上的两个动点,
上的两个动点, .
.
(1)若 ,求
,求 的值;
的值;
(2)求 的最小值.
的最小值.

【解析】第一问中解:设 ,
, 则
则
由 得
得 由
由 ,得
,得
 ②
②

第二问易求椭圆 的标准方程为:
的标准方程为:
 ,
,
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .
.
解:设 ,
, ……………………1分
……………………1分
则 ,由
,由 得
得 ①……2分
①……2分
(1)由 ,得
,得 ② ……………1分
② ……………1分
 ③ ………………………1分
③ ………………………1分
由①、②、③三式,消去 ,并求得
,并求得 .
………………………3分
.
………………………3分
(2)解法一:易求椭圆 的标准方程为:
的标准方程为: .………………2分
.………………2分
 , ……4分
, ……4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值 .…2分
.…2分
解法二: ,
………………4分
,
………………4分
所以,当且仅当 或
或 时,
时, 取最小值
取最小值
查看习题详情和答案>>
 的通项公式
的通项公式 ,
, ,试通过计算
,试通过计算 的值,推测出
的值,推测出 的值。
的值。 ,
,
 ,并根据结果可猜想
,并根据结果可猜想 。
。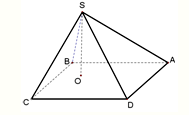 在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是
在四棱锥S-ABCD中,底面ABCD是边长为a的正方形,顶点S在底面内的射影O在正方形ABCD的内部(不在边上),且SO=λa,λ为常数,设侧面SAB,SBC,SCD,SDA与底面ABCD所成的二面角依次为α1,α2,α3,α4,则下列各式为常数的是