摘要：(i)因为对n∈N*恒成立.所以对n∈N*恒成立.
网址：http://m.1010jiajiao.com/timu_id_534918[举报]
已知f(x)=(x
+x)n，且正整数n满足
=
，A={0，1，2，…n}．
（1）求n；
（2）若i，j∈A，是否存在j，当i≥j时，
≤
恒成立．若存在，求出最小的j，若不存在，试说明理由：
（3）k∈A，若f（x）的展开式有且只有6个无理项，求k．
查看习题详情和答案>>
| 1 |
| k |
| C | 2 n |
| C | 6 n |
（1）求n；
（2）若i，j∈A，是否存在j，当i≥j时，
| C | i n |
| C | j n |
（3）k∈A，若f（x）的展开式有且只有6个无理项，求k．
已知f(x)=(x
+x)n，且正整数n满足Cn3=Cn5，A={0，1，2，…n}
（1）求n；
（2）若i、j∈A，是否存在j，当i≥j时，Cni≤Cnj恒成立．若存在，求出最小的j；若不存在，试说明理由．
（3）k∈A，若f（x）的展开式有且只有三个有理项，求k．
查看习题详情和答案>>
| 1 | k |
（1）求n；
（2）若i、j∈A，是否存在j，当i≥j时，Cni≤Cnj恒成立．若存在，求出最小的j；若不存在，试说明理由．
（3）k∈A，若f（x）的展开式有且只有三个有理项，求k．
设函数
（1）求函数y=T（x2）和y=（T（x））2的解析式；
（2）是否存在实数a，使得T（x）+a2=T（x+a）恒成立，若存在，求出a的值，若不存在，请说明理由；
（3）定义Tn+1（x）=Tn（T（x）），且T1（x）=T（x），（n∈N*）
①当
时，求y=T4（x）的解析式；
已知下面正确的命题：当
时（i∈N*，1≤i≤15），都有
恒成立．
②若方程T4（x）=kx恰有15个不同的实数根，确定k的取值；并求这15个不同的实数根的和．
查看习题详情和答案>>
（1）求函数y=T（x2）和y=（T（x））2的解析式；
（2）是否存在实数a，使得T（x）+a2=T（x+a）恒成立，若存在，求出a的值，若不存在，请说明理由；
（3）定义Tn+1（x）=Tn（T（x）），且T1（x）=T（x），（n∈N*）
①当
时，求y=T4（x）的解析式；已知下面正确的命题：当
时（i∈N*，1≤i≤15），都有恒成立．②若方程T4（x）=kx恰有15个不同的实数根，确定k的取值；并求这15个不同的实数根的和．
查看习题详情和答案>>
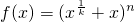，且正整数n满足Cn3=Cn5，A={0，1，2，…n}