摘要:当时.令.则.所以.
网址:http://m.1010jiajiao.com/timu_id_534786[举报]
如图所示,利用随机模拟的方法可以估计图中由y=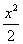 与两直线x=2及y=0所围成的阴影部分的面积S:
与两直线x=2及y=0所围成的阴影部分的面积S:
(1)先产生两组0~1的均匀随机数,a=RAND(),b=RAND();
(2)做变换,令x=2a,y=2b;
(3)产生N个点(x,y),并统计满足条件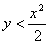 的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果当N=1000时N1=332,则据此可估计S=( )。
的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果当N=1000时N1=332,则据此可估计S=( )。
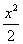 与两直线x=2及y=0所围成的阴影部分的面积S:
与两直线x=2及y=0所围成的阴影部分的面积S: (1)先产生两组0~1的均匀随机数,a=RAND(),b=RAND();
(2)做变换,令x=2a,y=2b;
(3)产生N个点(x,y),并统计满足条件
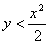 的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果当N=1000时N1=332,则据此可估计S=( )。
的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果当N=1000时N1=332,则据此可估计S=( )。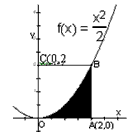
给出以下4个命题,其中所有正确结论的序号是
(1)当a为任意实数时,直线(a-1)x-y+2a+1=0恒过定点P则焦点在y轴上且过点P抛物线的标准方程是x2=
y.
(2)若直线l1:2kx+(k+1)y+1=0与直线l2:x-ky+2=0垂直,则实数k=1;
(3)已知数列{an}对于任意p,q∈N*,有ap+aq=ap+q,若a1=
,则a36=4
(4)对于一切实数x,令[x]大于x最大整数,例如:[3.05]=3,[
]=1,则函数f(x)=[x]称为高斯函数或取整函数,若an=f(
)(n∈N*),Sn为数列{an}的前n项和,则S50=145.
查看习题详情和答案>>
(1)(3)
(1)(3)
(1)当a为任意实数时,直线(a-1)x-y+2a+1=0恒过定点P则焦点在y轴上且过点P抛物线的标准方程是x2=
| 4 |
| 3 |
(2)若直线l1:2kx+(k+1)y+1=0与直线l2:x-ky+2=0垂直,则实数k=1;
(3)已知数列{an}对于任意p,q∈N*,有ap+aq=ap+q,若a1=
| 1 |
| 9 |
(4)对于一切实数x,令[x]大于x最大整数,例如:[3.05]=3,[
| 5 |
| 3 |
| n |
| 3 |
平面上两点F1,F2满足|F1F2|=4,设d为实数,令D表示平面上满足||PF1|-|PF2||=d的所有P点组成的图形,又令C为平面上以F1为圆心、6为半径的圆.则下列结论中,其中正确的有______(写出所有正确结论的编号).
①当d=0时,D为直线;
②当d=1时,D为双曲线;
③当d=2时,D与圆C交于两点;
④当d=4时,D与圆C交于四点;
⑤当d=4时,D不存在.
查看习题详情和答案>>
①当d=0时,D为直线;
②当d=1时,D为双曲线;
③当d=2时,D与圆C交于两点;
④当d=4时,D与圆C交于四点;
⑤当d=4时,D不存在.
 已知函数f(x)=
已知函数f(x)=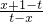 (t为常数).
(t为常数).
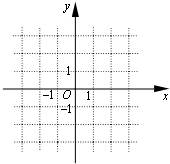
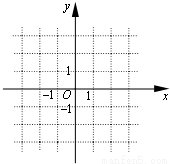
(1)当t=1时,在图中的直角坐标系内作出函数y=f(x)的大致图象,并指出该函数所具备的基本性质中的两个(只需写两个).
(2)设an=f(n)(n∈N*),当t>10,且t∉N*时,试判断数列{an}的单调性并由此写出该数列中最大项和最小项(可用[t]来表示不超过t的最大整数).
(3)利用函数y=f(x)构造一个数列{xn},方法如下:对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1)(n≥2,n∈N*),…在上述构造过程中,若xi(i∈N*)在定义域中,则构造数列的过程继续下去;若xi不在定义域中,则构造数列的过程停止.若取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数t的值.
查看习题详情和答案>>
已知函数f(x)=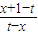 (t为常数).
(t为常数).
(1)当t=1时,在图中的直角坐标系内作出函数y=f(x)的大致图象,并指出该函数所具备的基本性质中的两个(只需写两个).
(2)设an=f(n)(n∈N*),当t>10,且t∉N*时,试判断数列{an}的单调性并由此写出该数列中最大项和最小项(可用[t]来表示不超过t的最大整数).
(3)利用函数y=f(x)构造一个数列{xn},方法如下:对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1)(n≥2,n∈N*),…在上述构造过程中,若xi(i∈N*)在定义域中,则构造数列的过程继续下去;若xi不在定义域中,则构造数列的过程停止.若取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数t的值.
 查看习题详情和答案>>
查看习题详情和答案>>
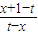 (t为常数).
(t为常数).(1)当t=1时,在图中的直角坐标系内作出函数y=f(x)的大致图象,并指出该函数所具备的基本性质中的两个(只需写两个).
(2)设an=f(n)(n∈N*),当t>10,且t∉N*时,试判断数列{an}的单调性并由此写出该数列中最大项和最小项(可用[t]来表示不超过t的最大整数).
(3)利用函数y=f(x)构造一个数列{xn},方法如下:对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1)(n≥2,n∈N*),…在上述构造过程中,若xi(i∈N*)在定义域中,则构造数列的过程继续下去;若xi不在定义域中,则构造数列的过程停止.若取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求实数t的值.
 查看习题详情和答案>>
查看习题详情和答案>>