摘要:(Ⅱ)当a=1时.证明:对任意的正整数n,当x≥2时.有f(x)≤x-1.(Ⅰ)解:由已知得函数f(x)的定义域为{x|x>1}.
网址:http://m.1010jiajiao.com/timu_id_534720[举报]
已知函数f(x)=ax+lnx,a∈R.
(I)当a=-1时,求f(x)的最大值;
(II)对f(x)图象上的任意不同两点P1(x1,x2),P(x2,y2)(0<x1<x2),证明f(x)图象上存在点P0(x0,y0),满足x1<x0<x2,且f(x)图象上以P0为切点的切线与直线P1P2平等;
(III)当a=
时,设正项数列{an}满足:an+1=f'(an)(n∈N*),若数列{a2n}是递减数列,求a1的取值范围.
查看习题详情和答案>>
(I)当a=-1时,求f(x)的最大值;
(II)对f(x)图象上的任意不同两点P1(x1,x2),P(x2,y2)(0<x1<x2),证明f(x)图象上存在点P0(x0,y0),满足x1<x0<x2,且f(x)图象上以P0为切点的切线与直线P1P2平等;
(III)当a=
| 3 | 2 |
已知函数f(x)=ax+bsinx,当x=
时,f(x)取得极小值
-
.
(1)求a,b的值;
(2)设直线l:y=g(x),曲线S:y=F(x).若直线l与曲线S同时满足下列两个条件:
①直线l与曲线S相切且至少有两个切点;
②对任意x∈R都有g(x)≥F(x).则称直线l为曲线S的“上夹线”.
试证明:直线l:y=x+2是曲线S:y=ax+bsinx的“上夹线”.
(3)记h(x)=
[5x-f(x)],设x1是方程h(x)-x=0的实数根,若对于h(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,问是否存在一个最小的正整数M,使得|h(x3)-h(x2)|≤M恒成立,若存在请求出M的值;若不存在请说明理由.
查看习题详情和答案>>
| π |
| 3 |
| π |
| 3 |
| 3 |
(1)求a,b的值;
(2)设直线l:y=g(x),曲线S:y=F(x).若直线l与曲线S同时满足下列两个条件:
①直线l与曲线S相切且至少有两个切点;
②对任意x∈R都有g(x)≥F(x).则称直线l为曲线S的“上夹线”.
试证明:直线l:y=x+2是曲线S:y=ax+bsinx的“上夹线”.
(3)记h(x)=
| 1 |
| 8 |
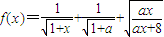 ,x∈(0,+∞).
,x∈(0,+∞).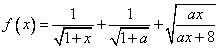 ,x∈(0,+∞),
,x∈(0,+∞),