题目内容
已知函数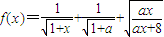 ,x∈(0,+∞).
,x∈(0,+∞).(1)当a=8时,求f(x)的单调区间;
(2)对任意正数a,证明:1<f(x)<2.
【答案】分析:(1)把a=8代入函数解析式,求出函数的导数,并判断导数的符号,得到函数的单调区间.
(2)令 ,则abx=8①,
,则abx=8①, ②,将f(x)解析式进行放缩,使用基本不等式,可证
②,将f(x)解析式进行放缩,使用基本不等式,可证
f(x)>1,由①、②式中关于x,a,b的对称性,不妨设x≥a≥b.则0<b≤2,当a+b≥7,将f(x)解析式进行放缩,可证
f(x)<2;当a+b<7③,将f(x)解析式进行放缩,再使用基本不等式证明f(x)<2.综上,1<f(x)<2.
解答:解:(1)、当a=8时,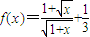 ,求得
,求得 ,
,
于是当x∈(0,1]时,f'(x)≥0;而当x∈[1,+∞)时,f'(x)≤0.
即f(x)在(0,1]中单调递增,而在[1,+∞)中单调递减.
(2).对任意给定的a>0,x>0,由 ,
,
若令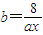 ,则abx=8①,
,则abx=8①,
而 ②
②
(一)先证f(x)>1;因为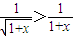 ,
, ,
, ,
,
又由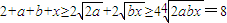 ,得a+b+x≥6.
,得a+b+x≥6.
所以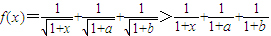
=

= .
.
(二)再证f(x)<2;由①、②式中关于x,a,b的对称性,不妨设x≥a≥b.则0<b≤2
(ⅰ)当a+b≥7,则a≥5,所以x≥a≥5,因为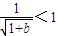 ,
,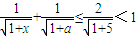 ,此时
,此时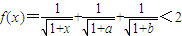 .
.
(ⅱ)当a+b<7③,由①得,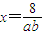 ,
, ,
,
因为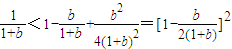
所以 ④
④
同理得 ⑤,
⑤,
于是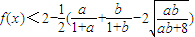 ⑥
⑥
今证明 ⑦,
⑦,
因为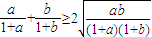 ,
,
只要证 ,即ab+8>(1+a)(1+b),也即a+b<7,据③,此为显然.
,即ab+8>(1+a)(1+b),也即a+b<7,据③,此为显然.
因此⑦得证.故由⑥得f(x)<2.
综上所述,对任何正数a,x,皆有1<f(x)<2.
点评:本题考查利用导数研究函数的单调性,用放缩法、基本不等式法证明不等式,体现分类讨论的数学思想.
(2)令
 ,则abx=8①,
,则abx=8①, ②,将f(x)解析式进行放缩,使用基本不等式,可证
②,将f(x)解析式进行放缩,使用基本不等式,可证f(x)>1,由①、②式中关于x,a,b的对称性,不妨设x≥a≥b.则0<b≤2,当a+b≥7,将f(x)解析式进行放缩,可证
f(x)<2;当a+b<7③,将f(x)解析式进行放缩,再使用基本不等式证明f(x)<2.综上,1<f(x)<2.
解答:解:(1)、当a=8时,
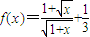 ,求得
,求得 ,
,于是当x∈(0,1]时,f'(x)≥0;而当x∈[1,+∞)时,f'(x)≤0.
即f(x)在(0,1]中单调递增,而在[1,+∞)中单调递减.
(2).对任意给定的a>0,x>0,由
 ,
,若令
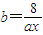 ,则abx=8①,
,则abx=8①,而
 ②
②(一)先证f(x)>1;因为
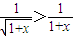 ,
, ,
, ,
,又由
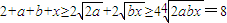 ,得a+b+x≥6.
,得a+b+x≥6.所以
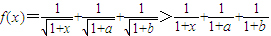
=


=
 .
.(二)再证f(x)<2;由①、②式中关于x,a,b的对称性,不妨设x≥a≥b.则0<b≤2
(ⅰ)当a+b≥7,则a≥5,所以x≥a≥5,因为
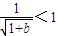 ,
,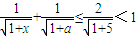 ,此时
,此时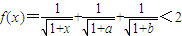 .
.(ⅱ)当a+b<7③,由①得,
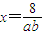 ,
, ,
,因为
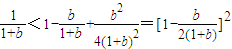
所以
 ④
④同理得
 ⑤,
⑤,于是
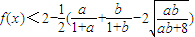 ⑥
⑥今证明
 ⑦,
⑦,因为
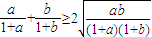 ,
,只要证
 ,即ab+8>(1+a)(1+b),也即a+b<7,据③,此为显然.
,即ab+8>(1+a)(1+b),也即a+b<7,据③,此为显然.因此⑦得证.故由⑥得f(x)<2.
综上所述,对任何正数a,x,皆有1<f(x)<2.
点评:本题考查利用导数研究函数的单调性,用放缩法、基本不等式法证明不等式,体现分类讨论的数学思想.

练习册系列答案
相关题目
