网址:http://m.1010jiajiao.com/timu_id_53335[举报]
已知点 (
( ),过点
),过点 作抛物线
作抛物线 的切线,切点分别为
的切线,切点分别为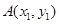 、
、 (其中
(其中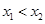 ).
).
(Ⅰ)若 ,求
,求 与
与 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,求圆
相切,求圆 的方程;
的方程;
(Ⅲ)若直线 的方程是
的方程是 ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切,
相切,
求圆 面积的最小值.
面积的最小值.
【解析】本试题主要考查了抛物线的的方程以及性质的运用。直线与圆的位置关系的运用。
中∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴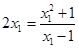 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
(3)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 ,借助于函数的性质圆
,借助于函数的性质圆 面积的最小值
面积的最小值
(Ⅰ)由 可得,
可得, . ------1分
. ------1分
∵直线 与曲线
与曲线 相切,且过点
相切,且过点 ,∴
,∴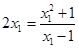 ,即
,即 ,
,
∴ ,或
,或 , --------------------3分
, --------------------3分
同理可得: ,或
,或 ----------------4分
----------------4分
∵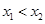 ,∴
,∴ ,
, . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,则
,则 的斜率
的斜率 ,
,
∴直线 的方程为:
的方程为: ,又
,又 ,
,
∴ ,即
,即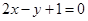 . -----------------7分
. -----------------7分
∵点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即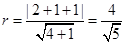 ,--------------8分
,--------------8分
故圆 的面积为
的面积为 . --------------------9分
. --------------------9分
(Ⅲ)∵直线 的方程是
的方程是 ,
, ,且以点
,且以点 为圆心的圆
为圆心的圆 与直线
与直线 相切∴点
相切∴点 到直线
到直线 的距离即为圆
的距离即为圆 的半径,即
的半径,即 , ………10分
, ………10分
∴
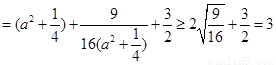 ,
,
当且仅当 ,即
,即 ,
, 时取等号.
时取等号.
故圆 面积的最小值
面积的最小值 .
.
查看习题详情和答案>>
已知函数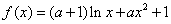 .
.
(Ⅰ)讨论函数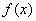 的单调性;
的单调性;
(Ⅱ)设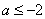 ,证明:对任意
,证明:对任意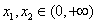 ,
,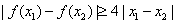 .
.
 1.选修4-1:几何证明选讲
1.选修4-1:几何证明选讲
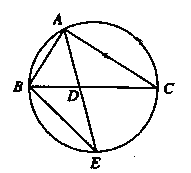
如图, 的角平分线
的角平分线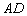 的延长线交它的外接圆于点
的延长线交它的外接圆于点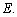
(Ⅰ)证明: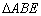 ∽△
∽△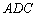 ;
;
(Ⅱ)若 的面积
的面积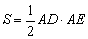 ,求
,求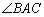 的大小.
的大小.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
则sin∠BAC=1,又∠BAC为三角形内角,所以∠BAC=90°.
查看习题详情和答案>>
已知函数 
 R).
R).
(Ⅰ)若  ,求曲线
,求曲线
 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
【解析】本试题主要考查了导数在研究函数中的运用。
第一问中,利用当 时,
时, .
.
 因为切点为(
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为:
第二问中,由题意得, 即
即 即可。
即可。
Ⅰ)当 时,
时, .
.
 ,
,
因为切点为( ),
则
),
则 ,
,
所以在点( )处的曲线的切线方程为:
)处的曲线的切线方程为: . ……5分
. ……5分
(Ⅱ)解法一:由题意得, 即
即 . ……9分
. ……9分
(注:凡代入特殊值缩小范围的均给4分)
 ,
,
因为 ,所以
,所以 恒成立,
恒成立,
故 在
在 上单调递增,
……12分
上单调递增,
……12分
要使 恒成立,则
恒成立,则 ,解得
,解得 .……15分
.……15分
解法二: ……7分
……7分
(1)当 时,
时, 在
在 上恒成立,
上恒成立,
故 在
在 上单调递增,
上单调递增,
 即
即 .
……10分
.
……10分
(2)当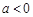 时,令
时,令 ,对称轴
,对称轴 ,
,
则 在
在 上单调递增,又
上单调递增,又
① 当 ,即
,即 时,
时, 在
在 上恒成立,
上恒成立,
所以 在
在 单调递增,
单调递增,
 即
即 ,不合题意,舍去
,不合题意,舍去
②当 时,
时, ,
不合题意,舍去 14分
,
不合题意,舍去 14分
综上所述:
查看习题详情和答案>>
已知函数
(1)若函数 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若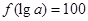 ,求a的值.
,求a的值.
【解析】本试题主要考查了指数函数的性质的运用。第一问中,因为函数 的图象经过P(3,4)点,所以
的图象经过P(3,4)点,所以 ,解得
,解得 ,因为
,因为 ,所以
,所以 .
.
(2)问中,对底数a进行分类讨论,利用单调性求解得到。
(3)中,由 知,
知, .,指对数互化得到
.,指对数互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函数 的图象经过
的图象经过 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵当 时,
时, ;
;
当 时,
时, . ……………… 6分
. ……………… 6分
因为, ,
,
当 时,
时, 在
在 上为增函数,∵
上为增函数,∵ ,∴
,∴ .
.
即 .当
.当 时,
时, 在
在 上为减函数,
上为减函数,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
查看习题详情和答案>>