网址:http://m.1010jiajiao.com/timu_id_53266[举报]
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 14 | 4 | 6 |
| 第三行 | 18 | 9 | 8 |
(I)求数列{an}和数列{bn}的通项公式;
(II)将数列{an}的项和数列{bn}的项依次从小到大排列得到数列{cn},数列{cn}的前n项和为Sn,试求最大的自然数M,使得当n≤M时,都有Sn≤2012.
(Ⅲ)若对任意n∈N,有an+1bn+λbnbn+1≥anbn+1成立,求实数λ的取值范围.
已知 是公差为d的等差数列,
是公差为d的等差数列, 是公比为q的等比数列
是公比为q的等比数列
(Ⅰ)若  ,是否存在
,是否存在 ,有
,有 ?请说明理由;
?请说明理由;
(Ⅱ)若 (a、q为常数,且aq
(a、q为常数,且aq 0)对任意m存在k,有
0)对任意m存在k,有 ,试求a、q满足的充要条件;
,试求a、q满足的充要条件;
(Ⅲ)若 试确定所有的p,使数列
试确定所有的p,使数列 中存在某个连续p项的和式数列中
中存在某个连续p项的和式数列中 的一项,请证明.
的一项,请证明.
【解析】第一问中,由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)中当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)中设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,
结合二项式定理得到结论。
解(1)由 得
得 ,整理后,可得
,整理后,可得
 、
、 ,
, 为整数
为整数 不存在
不存在 、
、 ,使等式成立。
,使等式成立。
(2)当 时,则
时,则
 即
即 ,其中
,其中 是大于等于
是大于等于 的整数反之当
的整数反之当 时,其中
时,其中 是大于等于
是大于等于 的整数,则
的整数,则 ,
,
显然 ,其中
,其中

 、
、 满足的充要条件是
满足的充要条件是 ,其中
,其中 是大于等于
是大于等于 的整数
的整数
(3)设 当
当 为偶数时,
为偶数时, 式左边为偶数,右边为奇数,
式左边为偶数,右边为奇数,
当 为偶数时,
为偶数时, 式不成立。由
式不成立。由 式得
式得 ,整理
,整理
当 时,符合题意。当
时,符合题意。当 ,
, 为奇数时,
为奇数时,

 由
由 ,得
,得

 当
当 为奇数时,此时,一定有
为奇数时,此时,一定有 和
和 使上式一定成立。
使上式一定成立。 当
当 为奇数时,命题都成立
为奇数时,命题都成立
查看习题详情和答案>>
如果一个实数数列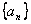 满足条件:
满足条件: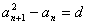 (
(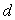 为常数,
为常数,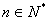 ),则称这一数列
“伪等差数列”,
),则称这一数列
“伪等差数列”, 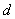 称为“伪公差”。给出下列关于某个伪等差数列
称为“伪公差”。给出下列关于某个伪等差数列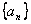 的结论:
的结论:
①对于任意的首项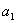 ,若
,若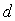 <0,则这一数列必为有穷数列;
<0,则这一数列必为有穷数列;
②当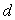 >0,
>0, 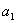 >0时,这一数列必为单调递增数列;
>0时,这一数列必为单调递增数列;
③这一数列可以是一个周期数列;
④若这一数列的首项为1,伪公差为3,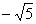 可以是这一数列中的一项;
可以是这一数列中的一项;
⑤若这一数列的首项为0,第三项为-1,则这一数列的伪公差可以是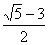 。
。
其中正确的结论是________________.
查看习题详情和答案>>
一支车队有15辆车,某天依次出发执行运输任务,第一辆车于下午2时出发,第二辆车于下午2时10分出发,第三辆车于下午2时20分出发,依此类推。假设所有的司机都连续开车,并都在下午6时停下来休息。
(1)到下午6时最后一辆车行驶了多长时间?
(2)如果每辆车的行驶速度都是60 ,这个车队当天一共行驶了多少千米?
,这个车队当天一共行驶了多少千米?
【解析】第一问中,利用第一辆车出发时间为下午2时,每隔10分钟即 小时出发一辆
小时出发一辆
则第15辆车在 小时,最后一辆车出发时间为:
小时,最后一辆车出发时间为: 小时
小时
第15辆车行驶时间为: 小时(1时40分)
小时(1时40分)
第二问中,设每辆车行驶的时间为: ,由题意得到
,由题意得到
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
则行驶的总时间为:
则行驶的总里程为: 运用等差数列求和得到。
运用等差数列求和得到。
解:(1)第一辆车出发时间为下午2时,每隔10分钟即 小时出发一辆
小时出发一辆
则第15辆车在 小时,最后一辆车出发时间为:
小时,最后一辆车出发时间为: 小时
小时
第15辆车行驶时间为: 小时(1时40分)
……5分
小时(1时40分)
……5分
(2)设每辆车行驶的时间为: ,由题意得到
,由题意得到
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
则行驶的总时间为: ……10分
……10分
则行驶的总里程为:
查看习题详情和答案>>
| 第一列 | 第二列 | 第三列 | |
| 第一行 | 3 | 2 | 10 |
| 第二行 | 14 | 4 | 6 |
| 第三行 | 18 | 9 | 8 |
(I)求数列{an}和数列{bn}的通项公式;
(II)将数列{an}的项和数列{bn}的项依次从小到大排列得到数列{cn},数列{cn}的前n项和为Sn,试求最大的自然数M,使得当n≤M时,都有Sn≤2012.
(Ⅲ)若对任意n∈N,有an+1bn+λbnbn+1≥anbn+1成立,求实数λ的取值范围.
查看习题详情和答案>>