(2)设切线的方程为:——青夏教育精英家教网——

摘要：(2)设切线的方程为:

网址：http://m.1010jiajiao.com/timu_id_530444[举报]

设圆C₁的方程为（x+2）²+（y-3m-2）²=4m²，直线l的方程为y=x+m+2．
（1）若m=1，求圆C₁上的点到直线l距离的最小值；
（2）求C₁关于l对称的圆C₂的方程；
（3）当m变化且m≠0时，求证：C₂的圆心在一条定直线上，并求C₂所表示的一系列圆的公切线方程．查看习题详情和答案>>

设圆C₁的方程为（x+2）²+（y-3m-2）²=4m²，直线l的方程为y=x+m+2．
（1）若m=1，求圆C₁上的点到直线l距离的最小值；
（2）求C₁关于l对称的圆C₂的方程；
（3）当m变化且m≠0时，求证：C₂的圆心在一条定直线上，并求C₂所表示的一系列圆的公切线方程．
查看习题详情和答案>>

设圆C₁的方程为（x+2）²+（y-3m-2）²=4m²，直线l的方程为y=x+m+2．
（1）若m=1，求圆C₁上的点到直线l距离的最小值；
（2）求C₁关于l对称的圆C₂的方程；
（3）当m变化且m≠0时，求证：C₂的圆心在一条定直线上，并求C₂所表示的一系列圆的公切线方程．
查看习题详情和答案>>

设圆C₁的方程为（x+2）²+（y-3m-2）²=4m²，直线l的方程为y=x+m+2．
（1）若m=1，求圆C₁上的点到直线l距离的最小值；
（2）求C₁关于l对称的圆C₂的方程；
（3）当m变化且m≠0时，求证：C₂的圆心在一条定直线上，并求C₂所表示的一系列圆的公切线方程．

查看习题详情和答案>>

设圆C₁的方程为，直线l的方程为，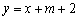

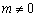(3) 当m为常值时，求C₁关于l对称的圆C₂的方程；

(4) 当m变化且时，求证：C₂的圆心在一条定直线上，并求C₂所表示的一系列圆的公切线方程．

查看习题详情和答案>>