摘要:(1)当时.则.此时.点适合题意.
网址:http://m.1010jiajiao.com/timu_id_530316[举报]
在 中,满足
中,满足 ,
, 是
是 边上的一点.
边上的一点.
(Ⅰ)若 ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值;
(Ⅱ)若 ,
, =m (m为正常数) 且
=m (m为正常数) 且 是
是 边上的三等分点.,求
边上的三等分点.,求 值;
值;
(Ⅲ)若 且
且 求
求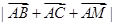 的最小值。
的最小值。
【解析】第一问中,利用向量的数量积设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求
为所求
第二问因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则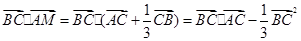 =
=
(2)当 时,则
时,则 =
=
第三问中,解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而
运用三角函数求解。
(Ⅰ)解:设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则 为所求……………2分
为所求……………2分
(Ⅱ)解:因为 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则 =
= ;-2分
;-2分
(2)当 时,则
时,则 =
= ;--2分
;--2分
(Ⅲ)解:设 ,因为
,因为
 ,
, ;
;
所以 即
即 于是
于是 得
得
从而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令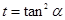 ,
, 则
则 ,则函数
,则函数 ,在
,在 递减,在
递减,在 上递增,所以
上递增,所以 从而当
从而当 时,
时,
查看习题详情和答案>>
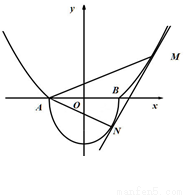
如图所示的曲线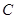 是由部分抛物线
是由部分抛物线 和曲线
和曲线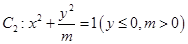 “合成”的,直线
“合成”的,直线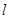 与曲线
与曲线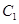 相切于点
相切于点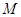 ,与曲线
,与曲线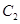 相切于点
相切于点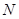 ,记点
,记点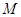 的横坐标为
的横坐标为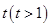 ,其中
,其中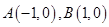 .
.
(1)当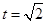 时,求
时,求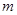 的值和点
的值和点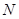 的坐标;
的坐标;
(2)当实数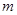 取何值时,
取何值时,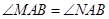 ?并求出此时直线
?并求出此时直线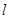 的方程.
的方程.
查看习题详情和答案>>
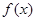 若存在
若存在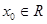 ,使
,使 成立,则称
成立,则称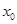 为
为
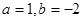 时,求
时,求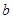 ,函数
,函数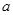 的取值范围。
的取值范围。