摘要:所以满足条件的的取值范围是.-------12分
网址:http://m.1010jiajiao.com/timu_id_526631[举报]
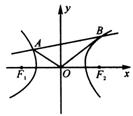
(本题满分12分)如图所示,F1、F2是双曲线x2 – y2 = 1的两个焦点,O为坐标原点,
圆O是以F??1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
 (Ⅰ)根据条件求出b和k的关系式;
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当![]() ,且满足2≤m≤4时,
,且满足2≤m≤4时,
求△AOB面积的取值范围.
查看习题详情和答案>>(本题满分12分)如图所示,F1、F2是双曲线x2 – y2 = 1的两个焦点,O为坐标原点,
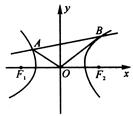
圆O是以F1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当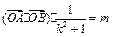 ,且满足2≤m≤4时,
,且满足2≤m≤4时,
求△AOB面积的取值范围.

圆O是以F1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当
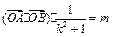 ,且满足2≤m≤4时,
,且满足2≤m≤4时,求△AOB面积的取值范围.
(2011•洛阳二模)给出下列命题:
①设向量
,
满足|
|=2,|
|=1,
,
的夹角为
.若向量2t
+7
与
+t
的夹角为钝角,则实数t的取值范围是(-7,-
);
②已知一组正数x1,x2,x3,x4的方差为s2=
(x12+x22+x32+x42)-4,则x1+1,x2+1,x3+1,x4+1的平均数为1
③设a,b,c分别为△ABC的角A,B,C的对边,则方程x2+2ax+b2=o与x2+2cx-b2=0有公共根的充要条件是A=90°;
④若f(n)表示n2+1(n∈N)的各位上的数字之和,如112+1=122,1+2+2=5,所以f(n)=5,记f1(n)=f(n),f2(n)=f[f1(n)],…fk+1(n)=f[fk(n)],k∈N,则f20(5)=11.
上面命题中,假命题的序号是
查看习题详情和答案>>
①设向量
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| π |
| 3 |
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
②已知一组正数x1,x2,x3,x4的方差为s2=
| 1 |
| 4 |
③设a,b,c分别为△ABC的角A,B,C的对边,则方程x2+2ax+b2=o与x2+2cx-b2=0有公共根的充要条件是A=90°;
④若f(n)表示n2+1(n∈N)的各位上的数字之和,如112+1=122,1+2+2=5,所以f(n)=5,记f1(n)=f(n),f2(n)=f[f1(n)],…fk+1(n)=f[fk(n)],k∈N,则f20(5)=11.
上面命题中,假命题的序号是
②
②
(写出所有假命题的序号).