摘要：得A=B或A+B=.但由于a≠b.∴A+B=
网址：http://m.1010jiajiao.com/timu_id_516300[举报]
解析：A错误．如图①所示，由两个结构相同的三棱锥叠放在一起构
成的几何体，各面都是三角形，但它不是棱锥．B错误．如答图②③所示，若△ABC不是直角三角形，或是直角三角形但旋转轴不是直角边，所得的几何体都不是圆锥．C错误．若六棱锥的所有棱都相等，则底面多边形是正六边形．由几何图形知，若以正六边形为底面，侧棱长必然要大于底面边长．D正确．
答案：D
查看习题详情和答案>>
按照某学者的理论，假设一个人生产某产品单件成本为a元，如果他卖出该产品的单价为m元，则他的满意度为
；如果他买进该产品的单价为n元，则他的满意度为
．如果一个人对两种交易（卖出或买进）的满意度分别为h1和h2，则他对这两种交易的综合满意度为
．现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙
（1）求h甲和h乙关于mA、mB的表达式；当mA=
mB时，求证：h甲=h乙；
（2）设mA=
mB，当mA、mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？
（3）记（2）中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由． 查看习题详情和答案>>
| m |
| m+a |
| a |
| n+a |
| h1h2 |
（1）求h甲和h乙关于mA、mB的表达式；当mA=
| 3 |
| 5 |
（2）设mA=
| 3 |
| 5 |
（3）记（2）中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由． 查看习题详情和答案>>
按照某学者的理论，假设一个人生产某产品单件成本为a元，如果他卖出该产品的单价为m元，则他的满意度为
；如果他买进该产品的单价为n元，则他的满意度为
．如果一个人对两种交易（卖出或买进）的满意度分别为h1和h2，则他对这两种交易的综合满意度为
．现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙
（1）求h甲和h乙关于mA、mB的表达式；当mA=
mB时，求证：h甲=h乙；
（2）设mA=
mB，当mA、mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？
（3）记（2）中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由．
查看习题详情和答案>>
| m |
| m+a |
| a |
| n+a |
| h1h2 |
（1）求h甲和h乙关于mA、mB的表达式；当mA=
| 3 |
| 5 |
（2）设mA=
| 3 |
| 5 |
（3）记（2）中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由．
按照某学者的理论，假设一个人生产某产品单件成本为a元，如果他卖出该产品的单价为m元，则他的满意度为
；如果他买进该产品的单价为n元，则他的满意度为
。如果一个人对两种交易（卖出或买进）的满意度分别为h1和h2，则他对这两种交易的综合满意度为
，现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙，
(1)求h甲和h乙关于mA，mB的表达式；当mA=
mB时，求证：h甲=h乙；
(2)设mA=mB，当mA，mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？
(3)记(2)中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由．
查看习题详情和答案>>
；如果他买进该产品的单价为n元，则他的满意度为。如果一个人对两种交易（卖出或买进）的满意度分别为h1和h2，则他对这两种交易的综合满意度为，现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙，(1)求h甲和h乙关于mA，mB的表达式；当mA=
mB时，求证：h甲=h乙；(2)设mA=
mB，当mA，mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？(3)记(2)中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由．
按照某学者的理论，假设一个人生产某产品单件成本为a元，如果他卖出该产品的单价为m元，则他的满意度为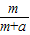
；如果他买进该产品的单价为n元，则他的满意度为
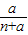．如果一个人对两种交易（卖出或买进）的满意度分别为h1和h2，则他对这两种交易的综合满意度为
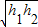．现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙
（1）求h甲和h乙关于mA、mB的表达式；当
时，求证：h甲=h乙；
（2）设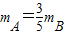
，当mA、mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？
（3）记（2）中最大的综合满意度为h，试问能否适当选取mA，mB的值，使得h甲≥h和h乙≥h同时成立，但等号不同时成立？试说明理由．
查看习题详情和答案>>
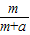；如果他买进该产品的单价为n元，则他的满意度为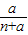．如果一个人对两种交易（卖出或买进）的满意度分别为h1和h2，则他对这两种交易的综合满意度为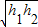．现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙（1）求h甲和h乙关于mA、mB的表达式；当
时，求证：h甲=h乙；（2）设
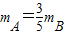，当mA、mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？（3）记（2）中最大的综合满意度为h，试问能否适当选取mA，mB的值，使得h甲≥h和h乙≥h同时成立，但等号不同时成立？试说明理由．
查看习题详情和答案>>