题目内容
按照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为 ;如果他买进该产品的单价为n元,则他的满意度为
;如果他买进该产品的单价为n元,则他的满意度为 。如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2,则他对这两种交易的综合满意度为
。如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2,则他对这两种交易的综合满意度为 ,现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mA元和mB元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙,
,现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mA元和mB元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙,
(1)求h甲和h乙关于mA,mB的表达式;当mA= mB时,求证:h甲=h乙;
mB时,求证:h甲=h乙;
(2)设mA= mB,当mA,mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
mB,当mA,mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
(3)记(2)中最大的综合满意度为h0,试问能否适当选取mA,mB的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立?试说明理由.
 ;如果他买进该产品的单价为n元,则他的满意度为
;如果他买进该产品的单价为n元,则他的满意度为 。如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2,则他对这两种交易的综合满意度为
。如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2,则他对这两种交易的综合满意度为 ,现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mA元和mB元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙,
,现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为mA元和mB元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙,(1)求h甲和h乙关于mA,mB的表达式;当mA=
 mB时,求证:h甲=h乙;
mB时,求证:h甲=h乙;(2)设mA=
 mB,当mA,mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
mB,当mA,mB分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h0,试问能否适当选取mA,mB的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立?试说明理由.
解:(1)
 ,
,
当mA= mB时,
mB时,
 ,
,
 ,
,
显然h甲=h乙。
(2)当mA= mB时,
mB时,

 ,
,
由 ,得
,得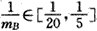 ,
,
故当 ,即mB=20,mA=12时,甲、乙两人同时取到最大的综合满意度为
,即mB=20,mA=12时,甲、乙两人同时取到最大的综合满意度为 。
。
(3)由(2)知 ,
,
由 ,
,
得
 ,
,
令 ,则
,则 ,即
,即
 ,
,
同理,由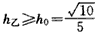 ,得
,得 ;
;
另一方面,
 ,
,
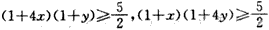 ,
,
当且仅当x ,即
,即 时取等号,
时取等号,
所以不能适当选取mA,mB的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立.

 ,
,当mA=
 mB时,
mB时, ,
, ,
,显然h甲=h乙。
(2)当mA=
 mB时,
mB时,
 ,
,由
 ,得
,得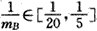 ,
,故当
 ,即mB=20,mA=12时,甲、乙两人同时取到最大的综合满意度为
,即mB=20,mA=12时,甲、乙两人同时取到最大的综合满意度为 。
。(3)由(2)知
 ,
,由
 ,
,得

 ,
,令
 ,则
,则 ,即
,即
 ,
,同理,由
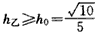 ,得
,得 ;
;另一方面,

 ,
,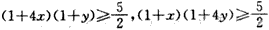 ,
,当且仅当x
 ,即
,即 时取等号,
时取等号,所以不能适当选取mA,mB的值,使得h甲≥h0和h乙≥h0同时成立,但等号不同时成立.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为 元,则他的满意度为
元,则他的满意度为 ;如果他买进该产品的单价为
;如果他买进该产品的单价为 元,则他的满意度为
元,则他的满意度为 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为 和
和 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为 .
.  元和
元和 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为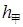 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为 .
. 时,求证:
时,求证: