网址:http://m.1010jiajiao.com/timu_id_51300[举报]
一、选择题
ADBBD ABBAD
二、填空题
11、 12、
12、 13、C
13、C 14、21 15、
14、21 15、 16、(-
16、(- ,0)
,0)
三、解答题
17、解:(1) 4分
4分
∵f(x)的最小值为3
所以-a+ =3,a=2
=3,a=2
∴f(x)=-2sin(2x+ )+5
6分
)+5
6分
(2)因为(- )变为了(
)变为了( ),所以h=
),所以h= ,k=-5
,k=-5
由图象变换得 =-2sin(2x-
=-2sin(2x- )
8分
)
8分
由2kp+ ≤2x-
≤2x- ≤2kp+
≤2kp+ 得kp+
得kp+ ≤x≤kp+
≤x≤kp+ 所以单调增区间为
所以单调增区间为
[kp+ , kp+
, kp+ ](k∈Z) 13分
](k∈Z) 13分
18、解:(1)如图,在四棱锥 中,
中,
∵BC∥AD,从而点D到平面PBC间的距离等于点A
到平面PBC的距离. 2分
∵∠ABC= ,∴AB⊥BC,
,∴AB⊥BC,
又PA⊥底面ABCD,∴PA⊥BC,
∴BC⊥平面 PAB, 4分
∴平面PAB⊥平面PBC,交线为PB,
过A作AE⊥PB,垂足为E,则AE⊥平面PBC,
∴AE的长等于点D到平面PBC的距离.
而 ,∴
,∴ .
.
即点D到平面PBC的距离为 .
6分
.
6分
(2)依题意依题意四棱锥P-ABCD的体积为 ,
,
∴(BC+AD)AB×PA= ,∴
,∴ ,
8分
,
8分
平面PDC在平面PAB上的射影为PAB,SPAB= ,
10分
,
10分
PC= ,PD=
,PD= ,DC=
,DC= ,SPDC=
,SPDC= a2,
12分
a2,
12分
设平面PDC和平面PAB所成二面角为q,则cosq= =
=
q=arccos . 13分
. 13分
19、解:(1)从10 道不同的题目中不放回地随机抽取3次,每次只抽取1道题,抽法总数为 只有第一次抽到艺术类数目的抽法总数为
只有第一次抽到艺术类数目的抽法总数为
∴ 5分
5分
(2)抽到体育类题目的可能取值为0,1,2,3则


∴ 的分布列为
的分布列为

0
1
2
3
P




10分
11分
从而有 13分
13分
20、解:(1)设 与
与 在公共点
在公共点 处的切线相同
处的切线相同
 1分
1分
由题意知 ,∴
,∴ 3分
3分
由 得,
得, ,或
,或 (舍去)
(舍去)
即有 5分
5分
(2)设 与
与 在公共点
在公共点 处的切线相同
处的切线相同

由题意知 ,∴
,∴
即有 8分
8分
令 ,则
,则 ,于是
,于是
当 ,即
,即 时,
时, ;
;
当 ,即
,即 时,
时, 11分
11分
21、解:(1)∵且|PF1|+|PF2|=
∴P的轨迹为以F1、F2为焦点的椭圆E,可设E:(其中b2=a2-5) 2分
在△PF
又
∴当且仅当| PF1 |=| PF2 |时,| PF1 |?| PF2 |取最大值, 4分
此时cos∠F1PF2取最小值
令= a2=9,
a2=9,
∵c= ∴b2=4故所求P的轨迹方程为 6分
(2)设N(s,t),M(x,y),则由,可得(x,y-3)=λ(s,t-3)
∴x=λs,y=3+λ(t-3) 7分
而M、N在动点P的轨迹上,故且
消去S得解得 10分
又| t |≤2,∴,解得,故λ的取值范围是[,5] 12分
22、解:(1)由 ,得
,得 ,代入
,代入 ,得
,得 ,
,
整理,得 ,从而有
,从而有 ,
, ,
,
 是首项为1,公差为1的等差数列,
是首项为1,公差为1的等差数列, 即
即 . 4分
. 4分
(2) ,
,  ,
,
 ,
,
 ,
,

 . 8分
. 8分
(3)∵


 .
.
由(2)知 ,
, ,
,




 .
12分
.
12分
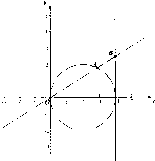 已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足
已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足| OM |
| OB |
| OM |
| AB |
(1)试用点M的坐标x,y表示y0,x1,y1;
(2)求动点M的轨迹方程F(x,y)=0;
(3)以下给出曲线C的五个方面的性质,请你选择其中的三个方面进行研究,并说明理由.(若你研究的方面多于三个,我们将只对试卷解答中的前三项予以评分)
①对称性;
②顶点坐标(定义:曲线与其对称轴的交点称为该曲线的顶点);
③图形范围;
④渐近线;
⑤对方程F(x,y)=0,当y≥0时,函数y=f(x)的单调性. 查看习题详情和答案>>
 直线l:y=k(x-1)过已知椭圆C:
直线l:y=k(x-1)过已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l交y轴于点M,且
| MA |
| AF |
| MB |
| BF |
(Ⅲ)连接AE、BD,试探索当直线l的倾斜角变化时,直线AE与BD是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由. 查看习题详情和答案>>

 ,或
,或 (舍去)
7分
(舍去)
7分
 的最大值为
的最大值为 ,故
,故 的最大值为
的最大值为 13分
13分