网址:http://m.1010jiajiao.com/timu_id_51279[举报]
说明:本评分标准每题只提供一种解法,如有其他解法,请参照本标准的精神给分.
一、填空题:本大题共14小题,每小题3分,共42分.
1.-7 2.12 3.50 4. 5.6 6.2 7.x≥2 8.
5.6 6.2 7.x≥2 8.
9.m<3 10.60
11.(4,-4) 12.4 13. 120 14.
二、选择题:本大题共4小题,每小题4分,共16分.
15.C 16.D 17.B 18.C
三、解答题:本大题共10小题,共92分.
19.(1)解:原式= ÷
÷ ……………………………………………………4分
……………………………………………………4分
=8 ÷4
÷4 =2.………………………………………………………………5分
=2.………………………………………………………………5分
(2)解:原式= …………………………………………………7分
…………………………………………………7分
= ………………………………………………………………9分
………………………………………………………………9分
= .………………………………………………………………10分
.………………………………………………………………10分
20.解:方程两边同乘以x(x+3)(x-1),得5(x-1)-(x+3)=0.…………………………2分
解这个方程,得 .……………………………………………………………………4分
.……………………………………………………………………4分
检验:把 代入最简公分母,得2×5×1=10≠0.
代入最简公分母,得2×5×1=10≠0.
∴原方程的解是 .……………………………………………………………………6分
.……………………………………………………………………6分
21.解: 过P作PC⊥AB于C点,根据题意,得
 AB=18×
AB=18× =6,∠PAB=90°-60°=30°,
=6,∠PAB=90°-60°=30°,
∠PBC=90°-45°=45°,∠PCB=90°,
∴PC=BC. ……………………………2分
在Rt△PAC中,
|
 ,解得PC=
,解得PC= . 6分
. 6分 的中点,∴OM⊥AB. …………………………………1分
的中点,∴OM⊥AB. …………………………………1分 过点O作OD⊥MN于点D,
过点O作OD⊥MN于点D, . ………………………3分
. ………………………3分 ,∴OD=
,∴OD= .
. ,…………………………………6分
,…………………………………6分 .…………………………………………………………………………2分
.…………………………………………………………………………2分 或
或 (不合题意,舍去).………………………………………4分
(不合题意,舍去).………………………………………4分 与
与 轴交点的纵坐标为-6,得
轴交点的纵坐标为-6,得 =-6.……………………1分
=-6.……………………1分 (6,6). …………………………3分
(6,6). …………………………3分 解这个方程组,得
解这个方程组,得 ……………………………………6分
……………………………………6分 .
. 25.解:(1)
25.解:(1) ,
, ,∴DE垂直平分AC,
,∴DE垂直平分AC, ,∠DFA=∠DFC =90°,∠DAF=∠DCF.……………………………1分
,∠DFA=∠DFC =90°,∠DAF=∠DCF.……………………………1分 ,即
,即 .∴AB?AF=CB?CD. ………………………………4分
.∴AB?AF=CB?CD. ………………………………4分 ,∴
,∴ .……………………………5分
.……………………………5分 (
( ). ………………………………………………7分
). ………………………………………………7分 ,
, ,得△DAF∽△ABC.
,得△DAF∽△ABC. ,EF=
,EF= .
. . ………………………………………………………11分
. ………………………………………………………11分 时,△PBC的周长最小,此时
时,△PBC的周长最小,此时 .………………………………12分
.………………………………12分 =8π,圆锥底面周长=2πr,∴圆的半径为4cm.………2分
=8π,圆锥底面周长=2πr,∴圆的半径为4cm.………2分 cm,而制作这样的圆锥实际需要正方形纸片的对角线长为
cm,而制作这样的圆锥实际需要正方形纸片的对角线长为 cm,
cm, ,
, , ①
, ①  . ② …………………………7分
. ② …………………………7分 ,
, . ………………9分
. ………………9分 cm,底面圆的半径为
cm,底面圆的半径为 cm. ………10分
cm. ………10分 中,得y=-2.
中,得y=-2. .……………………………………………………………………3分
.……………………………………………………………………3分 ,B(-2m,-
,B(-2m,- ),C(-2m,-n),E(-m,-n). ……………4分
),C(-2m,-n),E(-m,-n). ……………4分 ,S△DBO=
,S△DBO= ,S△OEN =
,S△OEN = . …………………………8分
. …………………………8分 ,得A(4,1),B(-4,-1),
,得A(4,1),B(-4,-1), ,由C、M两点在这条直线上,得
,由C、M两点在这条直线上,得 解得
解得 .
. .………………………………………………11分
.………………………………………………11分 设A点的横坐标为a,则B点的横坐标为-a.于是
设A点的横坐标为a,则B点的横坐标为-a.于是 .
. ,……………………………13分
,……………………………13分 .……………………14分
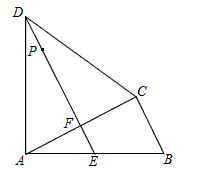
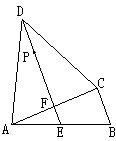
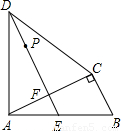
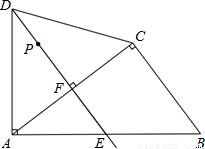
.……………………14分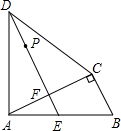 如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.已知AB=15cm,BC=9cm,P是射线DE上的动点.设DP=xcm(x>0),四边形BCDP的面积为ycm2.
如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE与AB相交于点E.已知AB=15cm,BC=9cm,P是射线DE上的动点.设DP=xcm(x>0),四边形BCDP的面积为ycm2. AF=CB
AF=CB CD
CD