摘要：2．若使代数式的值不小于的值.则的取值范围是 .
网址：http://m.1010jiajiao.com/timu_id_50879[举报]
(2004·湖北黄冈)(1)在2004年6月的日历中(如图所示)，任意圈出一竖列上相邻的三个数，设中间的一个为a，则用含a的代数式表示这三个数(从小到大排列)分别是________．
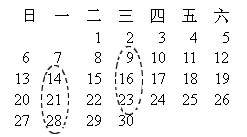
(2)现将连续自然数1～2 004按如图所示的方式排成一个长方形阵列，用一个正方形框出16个数．
①图中框出的这16个数的和是________．
②在图中，要使一个正方形框出的16个数之和分别等于2 000，2 004，是否可能？若不可能，试说明理由；若有可能，请求出该正方形框出的16个数中的最小值和最大数．
查看习题详情和答案>>
（本题8分）阅读下列材料：若关于
的一元二次方程
的两个实数根分别为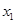
、
，则
， 
解决下面问题：已知关于x的一元二次方程
有两个非零不等实数根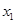、，设
.
【小题1】(1) 求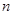
的取值范围；
【小题2】(2) 试用关于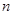的代数式表示出
；
【小题3】(3) 是否存在这样的
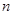值，使的值等于1？若存在，求出这样的所有的值；若不存在，请说明理由.
查看习题详情和答案>>
的一元二次方程 的两个实数根分别为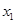、，则， 解决下面问题：已知关于x的一元二次方程
有两个非零不等实数根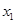、，设.【小题1】(1) 求
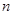的取值范围；【小题2】(2) 试用关于
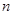的代数式表示出；【小题3】(3) 是否存在这样的
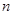值，使的值等于1？若存在，求出这样的所有的值；若不存在，请说明理由.
查看习题详情和答案>>
（本题8分）阅读下列材料：若关于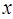
的一元二次方程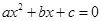
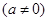的两个实数根分别为
、
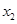，则
， 
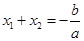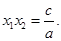
解决下面问题：已知关于x的一元二次方程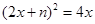
有两个非零不等实数根、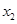，设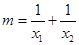
.
【小题1】(1) 求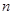
的取值范围；
【小题2】(2) 试用关于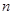的代数式表示出
；
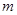【小题3】(3) 是否存在这样的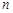
值，使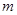的值等于1？若存在，求出这样的所有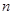的值；若不存在，请说明理由.
（本题8分）阅读下列材料：若关于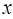
的一元二次方程
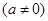的两个实数根分别为
、
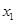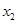，则
， 
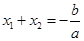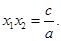
解决下面问题：已知关于x的一元二次方程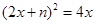
有两个非零不等实数根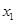、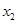，设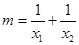
.
小题1:(1) 求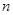
的取值范围；
小题2:(2) 试用关于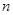的代数式表示出
；
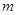小题3:(3) 是否存在这样的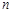
值，使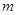的值等于1？若存在，求出这样的所有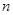的值；若不存在，请说明理由.
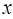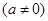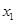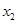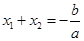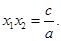
的一元二次方程 的两个实数根分别为、，则， 解决下面问题：已知关于x的一元二次方程
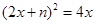有两个非零不等实数根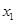、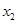，设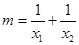.小题1:(1) 求
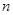的取值范围；小题2:(2) 试用关于
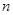的代数式表示出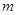；小题3:(3) 是否存在这样的
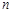值，使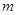的值等于1？若存在，求出这样的所有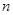的值；若不存在，请说明理由.
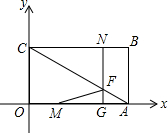在平面直角坐标系中，已知两点坐标P1（x1，y1）P2（x2，y2）我们就可以使用两点间距离公式P1P2=| (x1-x2)2+(y1-y 2)2 |
| (-1-0)2+(2-3)2 |
| 2 |
通过阅读材以上材料，请回答下列问题：
（1）已知点P1坐标为（-1，3），点P2坐标为（2，1）
①求P1P2=
| 13 |
| 13 |
②若点Q在x轴上，则△QP1P2的周长最小值为
6+
| 13 |
6+
．| 13 |
（2）如图，在平面直角坐标系中，四边形OABC为长方形，点A、B的坐标分别为
（4，0）（4，3），动点M、N分别从点O，点B同时出发，以每秒1个单位的速度运动，其中M点沿OA向终点A运动，N点沿BC向终点C运动，过点N作NF⊥BC交AC于F，交AO于G，连结MF．
当两点运动了t秒时：
①直接写出直线AC的解析式：
y=-
x+3
| 3 |
| 4 |
y=-
x+3
；| 3 |
| 4 |
②F点的坐标为（
4-t
4-t
，| 3 |
| 4 |
| 3 |
| 4 |
③记△MFA的面积为S，求S与t的函数关系式；（0＜t＜4）；
④当点N运动到终点C点时，在y轴上是否存在点E，使△EAN为等腰三角形？若存在，请直接写出点E的坐标，若不存在，请说明理由．