网址:http://m.1010jiajiao.com/timu_id_505040[举报]
1.  2. 1 3. 4 4.
2. 1 3. 4 4.  5. 1, 6. 90° 7. 13
5. 1, 6. 90° 7. 13
8.  9.
9.  10. 4
11. y=2x 12. 9
10. 4
11. y=2x 12. 9
13. D 14. B 15. D 16. C
17. 解: (1)y=2sin(2x- ),
), 
(2)

 ……
……
∴函数y的值域为[-1,2]
……………
18. (1)解 如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角
如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,则∠A′CP(或补角)为异面直线A′C与DE所成的角
在△A′CP中,
 易得A′C=
易得A′C= a,CP=DE=
a,CP=DE= a,A′P=
a,A′P= a
a
由余弦定理得cosA′CP=




(2)解 ∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上
∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上 如下图所示
如下图所示
 又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
故直线AD与平面B′EDF所成的角为∠ADB′
在Rt△B′AD中,AD= a,AB′=
a,AB′= a,B′D=
a,B′D= a
a
则cosADB′=
∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上 如下图所示
如下图所示
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
故直线AD与平面B′EDF所成的角为∠ADB′,
如图建立坐标系,则



 ,
,
19. (1)解 为等差数列,
为等差数列,
 ……………………………………………………2分
……………………………………………………2分
解得 ……………………………4分
……………………………4分
 ………………………………………………………………5分
………………………………………………………………5分
 ……………………………………………………………6分
……………………………………………………………6分
(2) ………………………………………………6分
………………………………………………6分

 …………8分
…………8分
因 ,知
,知 上单减,在
上单减,在 上单增,
上单增,
又 ,
,
而 …………………………………………10分
…………………………………………10分
∴当n =
5时, 取最大值为
取最大值为 ………………12分
………………12分
20. 解:(1)∵ ,∴
,∴ ,即
,即 ,
,
∵ ,∴
,∴
(2) ,
, 
当 ,
,
即 时,
时,
当 时,∵
时,∵ ,∴这样的
,∴这样的 不存在。
不存在。
当 ,即
,即 时,
时, ,这样的
,这样的 不存在。
不存在。
综上得,
 .
.
21. 解:(1) Q为PN的中点且GQ⊥PN
Q为PN的中点且GQ⊥PN
 GQ为PN的中垂线
GQ为PN的中垂线 |PG|=|GN|
|PG|=|GN|
∴|GN|+|GM|=|MP|=6,故G点的轨迹是以M、N为焦点的椭圆,其长半轴长 ,半焦距
,半焦距 ,∴短半轴长b=2,∴点G的轨迹方程是
,∴短半轴长b=2,∴点G的轨迹方程是
(2)因为 ,所以四边形OASB为平行四边形
,所以四边形OASB为平行四边形
若存在l使得| |=|
|=| |,则四边形OASB为矩形
|,则四边形OASB为矩形
若l的斜率不存在,直线l的方程为x=2,由
 矛盾,故l的斜率存在.
矛盾,故l的斜率存在.
设l的方程为

 ①
①

 ②
②
把①、②代入
∴存在直线 使得四边形OASB的对角线相等.
使得四边形OASB的对角线相等.
| π |
| 2 |
求(1)函数解析式,并利用“五点法”画出函数的图象;
(2)函数的最大值、以及达到最大值时x的集合;
(3)该函数图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩得到?
(4)当x∈(0,
| 3π |
| 2 |
(1)若函数y=f(x),x∈R是周期函数,写出符合条件a的值;
(2)求n≤x≤n+1(n≥0,n∈Z)时,求y=f(x)的表达式y=fn(x);
(3)若函数y=f(x)在[0,+∞)上的值域是闭区间,求a的取值范围.
查看习题详情和答案>>
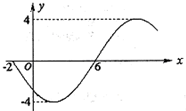 函数
函数