摘要：18．[方法一](1)证明:在线段BC1上取中点F.连结EF.DF则由题意得EF∥DA1.且EF=DA1.∴四边形EFDA1是平行四边形
网址：http://m.1010jiajiao.com/timu_id_504744[举报]
如图，在三棱柱ABCA1B1C1中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB＝3，BC＝5.
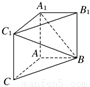
(1)求证：AA1⊥平面ABC；
(2)求二面角A1BC1B1的余弦值；
(3)证明：在线段BC1上存在点D，使得AD⊥A1B，并求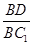
的值．
查看习题详情和答案>>
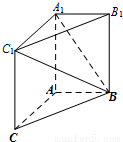
（2013•北京）如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1-BC1-B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求
| BD | BC1 |
如图，在三棱柱ABC-A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1-BC1-B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求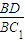
的值．
查看习题详情和答案>>
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1-BC1-B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求
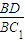的值．
查看习题详情和答案>>
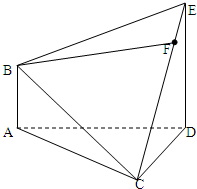在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1．