摘要:④第n个正三角形的不在第n-1个正三角形边上的顶点的横坐标是.则.其中正确结论的序号是 (把你认为正确结论的序号都填上).
网址:http://m.1010jiajiao.com/timu_id_504716[举报]
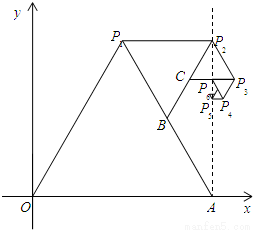
 (2009•孝感模拟)如图,O(0,0)A(1,0)为顶点作△OAP1,再以P1和P1A的中B为顶点作△P1BP2,再P2和P2B的中C为顶点作△P2CP3,…,如此继续下去.有如下结论:
(2009•孝感模拟)如图,O(0,0)A(1,0)为顶点作△OAP1,再以P1和P1A的中B为顶点作△P1BP2,再P2和P2B的中C为顶点作△P2CP3,…,如此继续下去.有如下结论:①所作的正三角形的边长构成公比为
| 1 |
| 2 |
②每一个正三角形都有一个顶点在直线AP2x=1)上;
③第六个正三角形的不在第五个正三角形边上的顶点P6的坐标是(
| 63 |
| 64 |
| 21 |
| 64 |
| 3 |
④第n个正三角形的不在第n-1个正三角形边上的顶点Pn的横坐标是xn,则
| lim |
| n→∞ |
其中正确结论的序号是
①②③④
①②③④
(把你认为正确结论的序号都填上).
如图,O(0,0)A(1,0)为顶点作△OAP1,再以P1和P1A的中B为顶点作△P1BP2,再P2和P2B的中C为顶点作△P2CP3,…,如此继续下去.有如下结论:
①所作的正三角形的边长构成公比为 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线AP2x=1)上;
③第六个正三角形的不在第五个正三角形边上的顶点P6的坐标是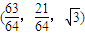 ;
;
④第n个正三角形的不在第n-1个正三角形边上的顶点Pn的横坐标是xn,则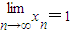 .
.
其中正确结论的序号是 (把你认为正确结论的序号都填上).
 查看习题详情和答案>>
查看习题详情和答案>>
①所作的正三角形的边长构成公比为
 的等比数列;
的等比数列;②每一个正三角形都有一个顶点在直线AP2x=1)上;
③第六个正三角形的不在第五个正三角形边上的顶点P6的坐标是
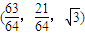 ;
;④第n个正三角形的不在第n-1个正三角形边上的顶点Pn的横坐标是xn,则
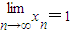 .
.其中正确结论的序号是 (把你认为正确结论的序号都填上).
 查看习题详情和答案>>
查看习题详情和答案>>
如图,以![]() 、
、![]() 为顶点作正
为顶点作正![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正
为顶点作正![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正
为顶点作正![]() ,…,如此继续下去.有如下结论:
,…,如此继续下去.有如下结论:
①所作的正三角形的边长构成公比为![]() 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线![]() (
(![]() )上;
)上;
③第六个正三角形的不在第五个正三角形边上的顶点![]() 的坐标是
的坐标是![]() ;
;
④第![]() 个正三角形的不在第
个正三角形的不在第![]() 个正三角形边上的顶点
个正三角形边上的顶点![]() 的横坐标是
的横坐标是![]() .
.
其中正确结论的序号是 (把你认为正确结论的序号都填上).

 :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
. 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; 上一点
上一点 经变换公式
经变换公式 与点
与点 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点