摘要:(2)若=1.且对任意正整数n,有,记.比较与T的大小关系.并给出证明, 的条件下.若不等式
网址:http://m.1010jiajiao.com/timu_id_501984[举报]
将正整数1,2,3,4,…,n2(n≥2)任意排成n行n列的数表.对于某一个数表,计算各行和各列中的任意两个数a,b(a>b)的比值 ,称这些比值中的最小值为这个数表的“特征值”.
,称这些比值中的最小值为这个数表的“特征值”.
(1)当n=2时,试写出排成的各个数表中所有可能的不同“特征值”;
(2)若aij表示某个n行n列数表中第i行第j列的数(1≤i≤n,1≤j≤n),且满足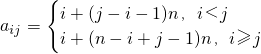 请分别写出n=3,4,5时数表的“特征值”,并由此归纳此类数表的“特征值”(不必证明);
请分别写出n=3,4,5时数表的“特征值”,并由此归纳此类数表的“特征值”(不必证明);
(3)对于由正整数1,2,3,4,…,n2排成的n行n列的任意数表,若某行(或列)中,存在两个数属于集合{n2-n+1,n2-n+2,…,n2},记其“特征值”为λ,求证: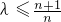 .
.
查看习题详情和答案>>
已知数列{an}中,a1=t,a2=t2(t>0且t≠1).若x=
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
(Ⅰ)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(Ⅱ)记bn=2(1-
),当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
(Ⅲ)当t=2时,求证:对于任意的正整数n,有
<
.
查看习题详情和答案>>
| t |
(Ⅰ)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(Ⅱ)记bn=2(1-
| 1 |
| an |
(Ⅲ)当t=2时,求证:对于任意的正整数n,有
| n |
 |
| k=1 |
| 2k |
| (ak+1)(ak+1+1) |
| 1 |
| 3 |
已知数列{an}中,a1=t,a2=t2(t>0且t≠1),若x=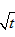 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。
(Ⅰ)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(Ⅱ)记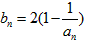 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
(Ⅲ)当t=2时,求证:对于任意的正整数n,有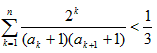 。
。
查看习题详情和答案>>
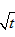 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点。(Ⅰ)证明数列{an+1-an}是等比数列,并求数列{an}的通项公式;
(Ⅱ)记
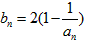 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;(Ⅲ)当t=2时,求证:对于任意的正整数n,有
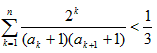 。
。 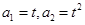 (t>0且t≠1).
(t>0且t≠1).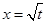 是函数
是函数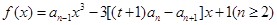 的一个极值点.
的一个极值点.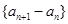 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;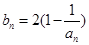 ,当t=2时,数列
,当t=2时,数列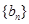 的前n项和为Sn,求使Sn>2012的n的最小值;
的前n项和为Sn,求使Sn>2012的n的最小值;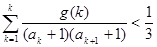 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.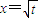 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.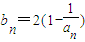 ,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;
,当t=2时,数列{bn}的前n项和为Sn,求使Sn>2008的n的最小值;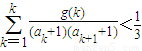 成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.
成立?若存在,求出满足条件的一个g(x);若不存在,请说明理由.