摘要:所以直线与平面所成角的正弦值为. ------14分解法二:
网址:http://m.1010jiajiao.com/timu_id_497443[举报]
 如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB.
如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB.(Ⅰ)求证:平面ABCD⊥平面APB;
(Ⅱ)求直线PC与平面PDB所成角的余弦值.
 如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB.
如图所示,ABCD是边长为a的正方形,△PBA是以角B为直角的等腰三角形,H为BD上一点,且AH⊥平面PDB.
(Ⅰ)求证:平面ABCD⊥平面APB;
(Ⅱ)求直线PC与平面PDB所成角的余弦值.
查看习题详情和答案>>
如图,四棱柱 中,
中,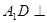 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 .
.

(1)求三棱锥 的体积;
的体积;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一点
上存在一点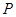 ,使得
,使得 ,当二面角
,当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值.
【解析】(1)在 中,
中,
 .
(3’)
.
(3’)
(2)以点D为坐标原点,建立如图所示的空间直角坐标系 ,则
,则
 (4’)
(4’)
 ,设平面
,设平面 的法向量为
的法向量为 ,
,
由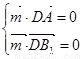 得
得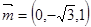 ,
(5’)
,
(5’)
则 ,
,
 . (7’)
. (7’)
(3)
设平面 的法向量为
的法向量为 ,由
,由 得
得 ,
(10’)
,
(10’)

查看习题详情和答案>>
已知正△ABC的顶点A在平面α上,顶点B,C在平面α的同一侧,D为BC的中点,若△ABC在平面α上的射影是以A为直角顶点的三角形,则直线AD与平面α所成角的正弦值的范围是( )
A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、(
|