摘要:所以当=时, 的最大值为5+4=9 -------
网址:http://m.1010jiajiao.com/timu_id_496943[举报]
已知幂函数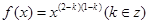 满足
满足 。
。
(1)求实数k的值,并写出相应的函数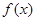 的解析式;
的解析式;
(2)对于(1)中的函数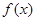 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数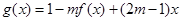 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
【解析】本试题主要考查了函数的解析式的求解和函数的最值的运用。第一问中利用,幂函数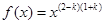 满足
满足 ,得到
,得到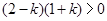
因为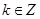 ,所以k=0,或k=1,故解析式为
,所以k=0,或k=1,故解析式为
(2)由(1)知,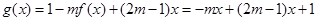 ,
, ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: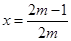 ,结合二次函数的对称轴,和开口求解最大值为5.,得到
,结合二次函数的对称轴,和开口求解最大值为5.,得到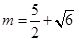
(1)对于幂函数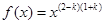 满足
满足 ,
,
因此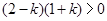 ,解得
,解得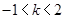 ,………………3分
,………………3分
因为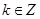 ,所以k=0,或k=1,当k=0时,
,所以k=0,或k=1,当k=0时, ,
,
当k=1时, ,综上所述,k的值为0或1,
,综上所述,k的值为0或1, 。………………6分
。………………6分
(2)函数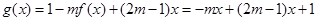 ,………………7分
,………………7分
由此要求 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: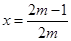 ,
,
当 时,
时,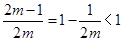 ,因为在区间
,因为在区间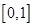 上的最大值为5,
上的最大值为5,
所以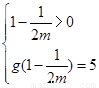 ,或
,或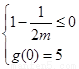 …………………………………………10分
…………………………………………10分
解得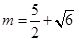 满足题意
满足题意
查看习题详情和答案>>
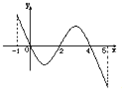 已知函数f(x)的定义域为?[-1,5],部分对应值如下表,f(x)的导函数 y?=f′(x)的图象如图所示,给出关于f(x)的下列命题:
已知函数f(x)的定义域为?[-1,5],部分对应值如下表,f(x)的导函数 y?=f′(x)的图象如图所示,给出关于f(x)的下列命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
②函数f(x)在[0,1]是减函数,在[1,2]是增函数,
③当1<a<2时,函数y=f(x)-a有4个零点
④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5,
其中所有正确命题序号为
①④
①④
.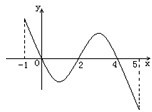 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
②函数f(x)在[0,1]是减函数,在[1,2]是增函数;
③当1<a<2时,函数y=f(x)-a有4个零点.
④如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为5.
其中所有正确命题序号为