摘要:(I)求边所在直线的方程,
网址:http://m.1010jiajiao.com/timu_id_496646[举报]
一、填空题(5分×12=60分)
1.--数学.files/image101.gif) 2.(-1,0) 3.(
2.(-1,0) 3.(--数学.files/image103.gif) )或(
)或(--数学.files/image105.gif) ) 4.
) 4.--数学.files/image107.gif)
5.4 6. --数学.files/image109.gif) 7.6 8.
7.6 8. --数学.files/image111.gif) 9.
9.--数学.files/image113.gif) 10.
10.--数学.files/image115.gif) 11. 120 12.(
11. 120 12.(--数学.files/image103.gif) )或(
)或(--数学.files/image105.gif) )
)
二、解答题
13.解:由已知--数学.files/image117.gif)
--数学.files/image119.gif)
(I)由已知
--数学.files/image121.gif)
--数学.files/image123.gif)
(II)|
=13-12sin(A+B)=13-12sin(2 B +--数学.files/image125.gif) ).
).
∵△ABC为锐角三角形,A-B=--数学.files/image125.gif) ,∴C=π-A-B<
,∴C=π-A-B<--数学.files/image128.gif) ,A=
,A=--数学.files/image125.gif) +B<
+B<--数学.files/image128.gif) .
.
--数学.files/image132.gif)
--数学.files/image134.gif)
--数学.files/image135.gif) 14.解:(I)因为
14.解:(I)因为--数学.files/image085.gif) 边所在直线的方程为
边所在直线的方程为--数学.files/image087.gif) ,且
,且--数学.files/image091.gif) 与
与--数学.files/image085.gif) 垂直,
垂直,
所以直线--数学.files/image091.gif) 的斜率为
的斜率为--数学.files/image142.gif) .又因为点
.又因为点--数学.files/image089.gif) 在直线
在直线--数学.files/image091.gif) 上,
上,
所以--数学.files/image091.gif) 边所在直线的方程为
边所在直线的方程为--数学.files/image147.gif) .
.--数学.files/image149.gif) .
.
(II)由--数学.files/image151.gif) 解得点
解得点--数学.files/image153.gif) 的坐标为
的坐标为--数学.files/image155.gif) ,
,
因为矩形--数学.files/image081.gif) 两条对角线的交点为
两条对角线的交点为--数学.files/image083.gif) .
.
所以--数学.files/image159.gif) 为矩形
为矩形--数学.files/image081.gif) 外接圆的圆心.
外接圆的圆心.
又--数学.files/image162.gif) .
.
从而矩形--数学.files/image081.gif) 外接圆的方程为
外接圆的方程为--数学.files/image165.gif) .
.
(III)因为动圆--数学.files/image095.gif) 过点
过点--数学.files/image168.gif) ,所以
,所以--数学.files/image170.gif) 是该圆的半径,又因为动圆
是该圆的半径,又因为动圆--数学.files/image095.gif) 与圆
与圆--数学.files/image159.gif) 外切,
外切,
所以--数学.files/image174.gif) ,即
,即--数学.files/image176.gif) .
.
故点--数学.files/image095.gif) 的轨迹是以
的轨迹是以--数学.files/image179.gif) 为焦点,实轴长为
为焦点,实轴长为--数学.files/image181.gif) 的双曲线的左支.
的双曲线的左支.
因为实半轴长--数学.files/image183.gif) ,半焦距
,半焦距--数学.files/image185.gif) .
.
所以虚半轴长--数学.files/image187.gif) .
.
从而动圆--数学.files/image095.gif) 的圆心的轨迹方程为
的圆心的轨迹方程为--数学.files/image190.gif) .
.
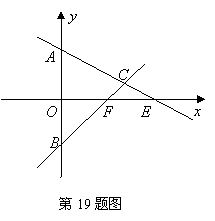
 已知△ABC的顶点A(0,2),AC边上的高线BD所在直线的方程为x-2y+2=0,∠ABC的角平分线所在的直线方程为y=0.求:
已知△ABC的顶点A(0,2),AC边上的高线BD所在直线的方程为x-2y+2=0,∠ABC的角平分线所在的直线方程为y=0.求:(I)直线AC的方程;
(Ⅱ)点C到直线AB的距离.
已知△ABC的顶点A(0,2),AC边上的高线BD所在直线的方程为x-2y+2=0,∠ABC的角平分线所在的直线方程为y=0.求:
(I)直线AC的方程;
(Ⅱ)点C到直线AB的距离.
 查看习题详情和答案>>
查看习题详情和答案>>
(I)直线AC的方程;
(Ⅱ)点C到直线AB的距离.
 查看习题详情和答案>>
查看习题详情和答案>>
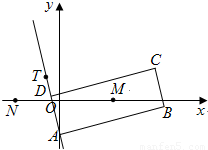
 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.(I)求矩形ABCD外接圆的方程;
(Ⅱ)若直线l经过点N(-2,0),且与矩形ABCD的外接圆有公共点,求直线的倾斜角的范围.
 时点
时点