网址:http://m.1010jiajiao.com/timu_id_492421[举报]
A.必做题部分
一、填空题:(本大题共14小题,每小题5分,共70分.)
1. 2.
2. 3.共线 4.20 5.
3.共线 4.20 5. 6.
6. 7.
7. 8.2,5,10 9.16.4 10.1 11.7 12.
8.2,5,10 9.16.4 10.1 11.7 12. 13.2 14.
13.2 14.
二、解答题:
15.解:(1)

(2)
余弦定理 可得
可得
又∵
∴
16.证明 (1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD内的射影,
(1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD内的射影,
(2)取CD中点G,连EG、FG,
∵E、F分别是AB、PC的中点,∴EG∥AD,FG∥PD
∴平面EFG∥平面PAD,故EF∥平面PAD
(3)解 当平面PCD与平面ABCD成45°角时,直线EF⊥面PCD
当平面PCD与平面ABCD成45°角时,直线EF⊥面PCD
证明 G为CD中点,则EG⊥CD,由(1)知FG⊥CD,故∠EGF为平面PCD与平面ABCD所成二面角的平面角
G为CD中点,则EG⊥CD,由(1)知FG⊥CD,故∠EGF为平面PCD与平面ABCD所成二面角的平面角 即∠EGF=45°,从而得∠ADP=45°,AD=AP
即∠EGF=45°,从而得∠ADP=45°,AD=AP
由Rt△PAE≌Rt△CBE,得PE=CE
又F是PC的中点,∴EF⊥PC,由CD⊥EG,CD⊥FG,得CD⊥平面EFG,CD⊥EF即EF⊥CD,故EF⊥平面PCD
17.解:(1)依题意, 到
到 距离等于
距离等于 到直线
到直线 的距离,曲线
的距离,曲线 是以原点为顶点,
是以原点为顶点, 为焦点的抛物线
为焦点的抛物线
 曲线
曲线 方程是
方程是
(2)设圆心 ,因为圆
,因为圆 过
过
故设圆的方程
令 得:
得:
设圆与 轴的两交点为
轴的两交点为 ,则
,则

 在抛物线
在抛物线 上,
上,


所以,当 运动时,弦长
运动时,弦长 为定值2
为定值2
18.解(1)设日销售量为
则日利润
(2)
 ①当2≤a≤4时,33≤a+31≤35,当35 <x<41时,
①当2≤a≤4时,33≤a+31≤35,当35 <x<41时,
∴当x=35时,L(x)取最大值为
②当4<a≤5时,35≤a+31≤36,
易知当x=a+31时,L(x)取最大值为 综合上得
综合上得
19.解(1)据题意: 
可行域如图(暂缺)
 的几何意义是定点
的几何意义是定点 到区域内的点
到区域内的点 连线的斜率
连线的斜率 ,
,
又
故 的取值范围为
的取值范围为
(2)当 有零点时,
有零点时, ,满足条件为
,满足条件为
由抛物线的下方与 围成的区域面积
围成的区域面积

由直线 围成的区域面积
围成的区域面积
故 有零点的概率
有零点的概率

 无零点的概率为
无零点的概率为
(3) 是
是 函数.
函数.
证明:  符合条件.
符合条件.
因为 ,
,
同理: ;
;



 .
.
所以,  符合条件.
符合条件.
20.(1)解:由已知:对于 ,总有
,总有 ①成立
①成立
∴ (n ≥ 2)②
(n ≥ 2)②
①--②得
∴
∵ 均为正数,∴
均为正数,∴ (n ≥ 2)
(n ≥ 2)
∴数列 是公差为1的等差数列
又n=1时,
是公差为1的等差数列
又n=1时, ,
解得
,
解得 =1
=1
∴ .(
.( )
)
(2)证明:∵对任意实数 和任意正整数n,总有
和任意正整数n,总有 ≤
≤ .……6分
.……6分
∴

(3)解:由已知  ,
,

易得 
猜想 n≥2 时, 是递减数列.
是递减数列.
令
∵当
∴在 内
内 为单调递减函数.
为单调递减函数.
由 .
.
∴n≥2 时,  是递减数列.即
是递减数列.即 是递减数列.
是递减数列.
又 , ∴数列
, ∴数列 中的最大项为
中的最大项为 .
.
B.附加题部分
三、附加题部分:
21.(必做题)(本小题满分12分)
解:(1)将 代入
代入 得
得 ,
,
由△ 可知
可知 ,
,
另一方面,弦长AB ,解得
,解得 ;
;
(2)当 时,直线为
时,直线为 ,要使得内接△ABC面积最大,
,要使得内接△ABC面积最大,
则只须使得 ,
,
即 ,即
,即 位于(4,4)点处.
位于(4,4)点处.
22.(必做题)(本小题满分12分)
解:(1)分别记甲、乙、丙三个同学笔试合格为事件 、
、 、
、 ;
;
 表示事件“恰有一人通过笔试”
表示事件“恰有一人通过笔试”
则


(2)解法一:因为甲、乙、丙三个同学经过两次考试后合格的概率均为 ,
,
所以 ,故
,故 .
.
解法二:分别记甲、乙、丙三个同学经过两次考试后合格为事件 ,
,
则
所以 ,
,
 ,
, .
.
于是, .
.
23.(选做题)(本小题满分8分)
证明:(1)过D点作DG∥BC,并交AF于G点,
∵E是BD的中点,∴BE=DE,
又∵∠EBF=∠EDG,∠BEF=∠DEG,
∴△BEF≌△DEG,则BF=DG,
∴BF:FC=DG:FC,
又∵D是AC的中点,则DG:FC=1:2,
则BF:FC=1:2;
(2)若△BEF以BF为底,△BDC以BC为底,
则由(1)知BF:BC=1:3,
又由BE:BD=1:2可知 :
: =1:2,其中
=1:2,其中 、
、 分别为△BEF和△BDC的高,
分别为△BEF和△BDC的高,
 则
则 ,则
,则 =1:5.
=1:5.
24.(选做题)(本小题满分8分)
解:(1)消去参数 ,得直线
,得直线 的普通方程为
的普通方程为 ;-----------------------2分
;-----------------------2分
 即
即 ,
,
两边同乘以 得
得 ,
,
消去参数 ,得⊙
,得⊙ 的直角坐标方程为:
的直角坐标方程为:

(2)圆心 到直线
到直线 的距离
的距离 ,
,
所以直线 和⊙
和⊙ 相交.
相交.
25.(选做题)(本小题满分8分)
解:MN = 
 =
= ,
,
即在矩阵MN变换下 ,
,
则 ,
,
即曲线 在矩阵MN变换下的函数解析式为
在矩阵MN变换下的函数解析式为 .
.
26.(选做题)(本小题满分8分)
证明:(1)当 时,左边=
时,左边= ,
,
 时成立
时成立
(2)假设当 时成立,即
时成立,即
那么当 时,左边
时,左边



 时也成立
时也成立
根据(1)(2)可得不等式对所有的 都成立
都成立
(本小题为选做题,满分8分)
已知直线![]() 的参数方程:
的参数方程:![]() (
(![]() 为参数)和圆
为参数)和圆![]() 的极坐标方程:
的极坐标方程:
![]() .
.
(1)将直线![]() 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)判断直线![]() 和圆
和圆![]() 的位置关系.
的位置关系.
(本小题满分12分)
某单位组织50名志愿者利用周末和节假日参加社会公益活动,活动内容是:1、到各社区宣传慰问,创导文明新风;2、到指定的社区、车站、码头做义工,帮助那些需要帮助的人。各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
|
|
宣传慰问 |
义工救助 |
总计 |
|
20至40岁 |
11 |
16 |
27 |
|
大于40岁 |
15 |
8 |
23 |
|
总计 |
26 |
24 |
50 |
(Ⅰ) 用分层抽样方法在做义工的志愿者中随机抽取6名,大于40岁的应该抽取几名?

(Ⅱ) 在上述抽取的6名志愿者中任取2名,求恰有1名志愿者年龄大于40岁的概率.
(Ⅲ)如果“宣传慰问”与“做义工”是两个分类变量,并且计算出随机变量 ,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
,那么你有多大的把握认为选择做宣传慰问与做义工是与年龄有关系的?
查看习题详情和答案>>
 平面ABCD且CD⊥AD,∴CD⊥PD
平面ABCD且CD⊥AD,∴CD⊥PD .
.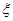 的分布列,并计算其数学期望.
的分布列,并计算其数学期望.