摘要：(2) 当(0,1]时, 若的图象上任意一点处的切线的倾斜角为,求当时的取值范围.
网址：http://m.1010jiajiao.com/timu_id_49233[举报]
一、选择题：本大题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有 一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题：（本大题共5个小题，每小题5分，共25分，）
11． 12. 13. 14. 15.
三、解答题：
已知函数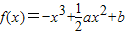
．
（1）若y=f（x）在x=1处的极值为
，求y=f（x）的解析式并确定其单调区间；
（2）当x∈（0，1]时，若y=f（x）的图象上任意一点处的切线的倾斜角为θ，求当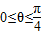
时a的取值范围．
查看习题详情和答案>>
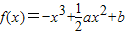．（1）若y=f（x）在x=1处的极值为
，求y=f（x）的解析式并确定其单调区间；（2）当x∈（0，1]时，若y=f（x）的图象上任意一点处的切线的倾斜角为θ，求当
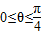时a的取值范围．查看习题详情和答案>>
已知二次函数f（x）满足：①当x=2时有极值；②图象与y轴交点的纵坐标为-4，且在该点处的切线与直线4x+y-4=0平行．
（1）求f（-1）的值；
（2）若m∈R，求函数y=F（xlnx+m），x∈[1，e]的最小值；
（3）若曲线y=f（lnx），x∈（1，+∞）上任意一点处的切线的斜率恒大于k3-k-4，求k的取值范围．
查看习题详情和答案>>
已知函数f(x)=-x3+
ax2+b．
（1）若y=f（x）在x=1处的极值为
，求y=f（x）的解析式并确定其单调区间；
（2）当x∈（0，1]时，若y=f（x）的图象上任意一点处的切线的倾斜角为θ，求当0≤θ≤
时a的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
（1）若y=f（x）在x=1处的极值为
| 5 |
| 2 |
（2）当x∈（0，1]时，若y=f（x）的图象上任意一点处的切线的倾斜角为θ，求当0≤θ≤
| π |
| 4 |
已知函数f（x）=mx3+nx2（m、n∈R，m≠0）的图象在（2，f（2））处的切线与x轴平行．
（1）求n，m的关系式并求f（x）的单调减区间；
（2）证明：对任意实数0＜x1＜x2＜1，关于x的方程：f′(x)-
=0在（x1，x2）恒有实数解
（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f（x）是在闭区间[a，b]上连续不断的函数，且在区间（a，b）内导数都存在，则在（a，b）内至少存在一点x0，使得f′(x0)=
．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
当0＜a＜b时，
＜ln
＜
（可不用证明函数的连续性和可导性）．
查看习题详情和答案>>
（1）求n，m的关系式并求f（x）的单调减区间；
（2）证明：对任意实数0＜x1＜x2＜1，关于x的方程：f′(x)-
| f(x2)-f(x1) |
| x2-x1 |
（3）结合（2）的结论，其实我们有拉格朗日中值定理：若函数f（x）是在闭区间[a，b]上连续不断的函数，且在区间（a，b）内导数都存在，则在（a，b）内至少存在一点x0，使得f′(x0)=
| f(b)-f(a) |
| b-a |
当0＜a＜b时，
| b-a |
| b |
| b |
| a |
| b-a |
| a |
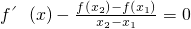在（x1，x2）恒有实数解
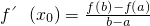．如我们所学过的指、对数函数，正、余弦函数等都符合拉格朗日中值定理条件．试用拉格朗日中值定理证明：
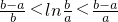（可不用证明函数的连续性和可导性）．